In the parallogram triangles ABC and ACD are equal in area because they're congruent:
AB=DC and AD=BC (opposite sides have equal length and both triangles ar between the same parallel lines AB and DC so they have equal area. Area of ACD=CDF+ACF and ABC=BCE+ACE. So (i) and (ii) are related by this commonality.
(i)
DF/AD=FG/AH (reduction in height CDF and ACD),
BE/AB=EQ/AP (reduction in height BCE and ABC).
Area BCE/area ABC=EQ/AP=BE/AB (triangle ABP),
Area CDF/area ACD=FG/AH=DF/AD (triangle ADH).
AE+BE=AB, AF+DF=AD.
AF/AD+EQ/AP=AE/AB+BE/AB=(AE+BE)/AB=AB/AB=1.
AE/AB+FG/AH=AF/AD+DF/AD=(AF+DF)/AD=AD/AD=1.
EQ/AP=1-AF/AD and FG/AH=1-AE/AB. But AE/AB=AF/AD therefore EQ/AP=FG/AH.
Since the heights of the triangles (of equal area initially) are reduced by the same amount, their areas are also so reduced. This makes them equal in area.
In the picture, the heights of the triangles are shown by the perpendiculars FG, AH, EQ, AP.
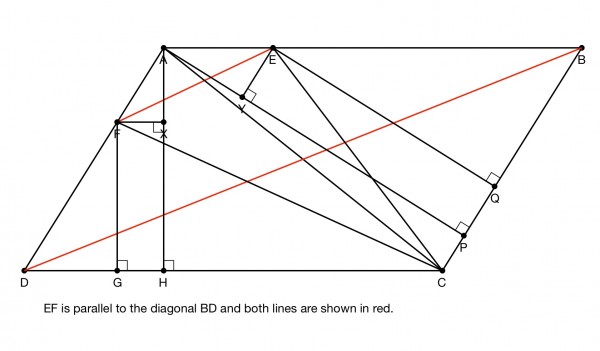
For part (ii), having established (i) and knowing that the area of ACD=CDF+ACF and ABC=BCE+ACE, the areas of ACF and ACE are also equal.