This answer has been revised as a result of comments and corrections and is now believed to be correct.
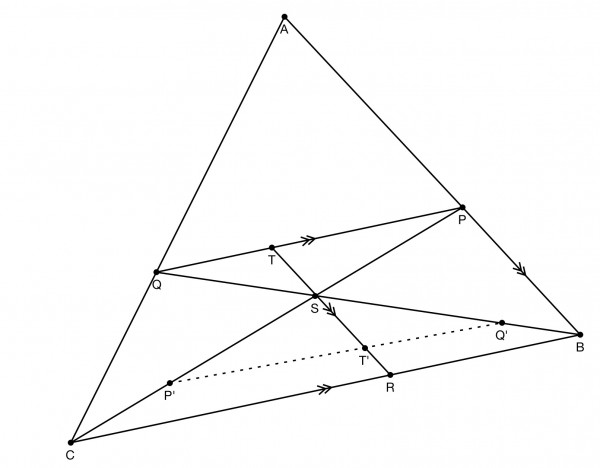
Point T has been inserted as the intersection of RS extended to meet PQ.
Similar triangles ABC and APQ: AQ/AC=PQ/BC.
To make it easier to see the similar triangles PQS and BCS, the points P', Q' and T' have been inserted such that P'Q' is the same length as PQ, making triangles PQS and P'Q'S congruent. It's then easier to appreciate the ratios of the sides of the similar triangles, because ST=S'T', PS=P'S, etc.
Similar triangles PQS and BCS: PQ/BC=QS/BS=PS/CS (angles QPS=BCS, PQS=CBS, PSQ=BSC, alternate angles between parallel lines). With the introduction of the extra points, we can also write P'Q'/BC=Q'S/BS=P'S/CS.
BR=PT in parallelogram BRTP and PT=P'T'. AQ/AC=PQ/BC=(PT+QT)/(BR+CR)=(BR+QT)/(BR+CR).
P'T'/CR=Q'T'/BR so PT/CR=QT/BR, because ST'/RS=ST/RS is a common ratio in triangles P'ST' and CRS, and Q'ST' and BRS.
But BR=PT so BR/CR=QT/BR, QT=BR^2/CR and AQ/AC=PQ/BC=(BR+BR^2/CR)/(BR+CR)=BR(CR+BR)/(CR(BR+CR))=BR/CR. Hence AQ/AC=BR/CR, in other words BR/RC=AQ/AC.