Complete the squares:
25(x²+2x+1)-25 + 169(y²-4y+4)-676=3524.
25(x+1)²+169(y-2)²=3524+25+676=4225.
Divide through by 4225:
(x+1)²/169+(y-2)²/25=1.
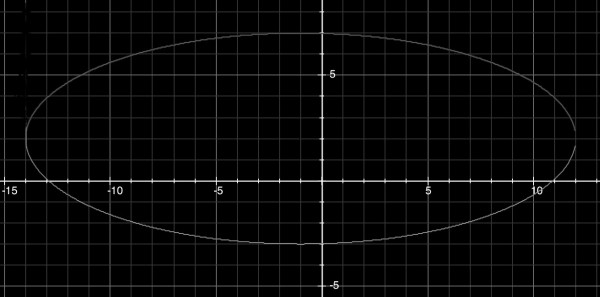
(x+1)²/13²+(y-2)²/5²=1.
This is the equation of an ellipse with semi-major axis, a=13 and semi-minor axis, b=5.
Centre is (-1,2).
Vertices at (-1±13,2) and (-1,2±5), that is, (12,2), (-14,2), (-1,7), (-1,-3).
Length of focus from centre of ellipse is given by f²=√(a²-b²)=√169-25=√144=12.
Foci at (-1±12,2), that is, (11,2) and (-13,2).