First, here’s what the graph looks like:
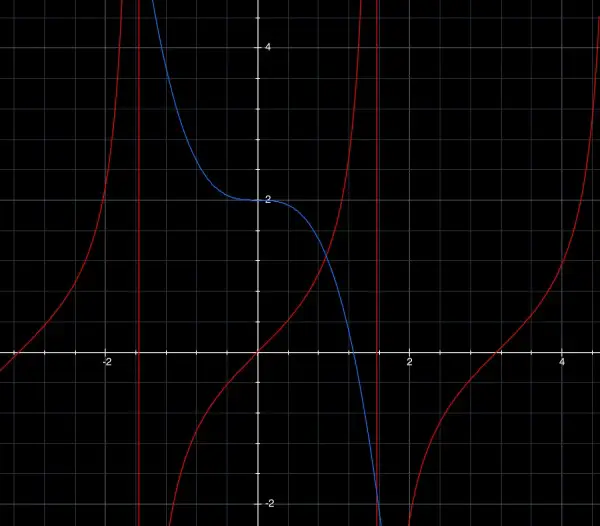
The red curve is y=tan(x) where x is in radians. The vertical red lines are asymptotes at x=nπ/2=1.5708n (approx) where n is an odd integer (positive and negative). The blue curve is y=2-x³. The first quadrant is marked by the y axis and the first positive asymptote at x=1.5708.
I guess that the lines specified in a) through f) are the axes around which the curves are to be rotated, acting like spindles through the centre of the solid body of the rotated figure.
For part a) we are looking at the shape bounded by the red curve, the blue curve and the x-axis, which resembles a curvy triangle with an apex formed by the intersection of the red and blue curves. We can split the volume of the rotated shape by breaking it down into two components separated by the vertical line passing through the intersection of red and blue. We need to find the coords of the intersection, or rather, the x coord, so that we have limits for the integration. The x coord is found by solving 2-x³=tan(x). I can do this on my calculator and I get x=0.9021550497 approx. For the sake of illustration let’s call this x=0.9. The point is that we only need the red curve to find the volume of the left component and only the blue curve for the right component, which also requires us to find where the blue curve intersects the x-axis, that is, at x=∛2.
Now to work out the integral expressions. In each case a), b), c) we use the vertical height (the y-coord) of the red or blue curve above the x-axis. This is the radius of an infinitesimally thin disc with volume πy²dx where dx is the thickness of the disc. The sum total of the volumes of all discs is the integral, with limits for x of 0 and 0.9 or 0.9 and ∛2 for the left or right components respectively. We replace y by tan(x) so that we end up with a left component of π∫tan²(x)dx between 0 and 0.9; and a right component of π∫(2-x³)²dx between 0.9 and ∛2.
b) Note that y=a where a>8 is way above the blue curve for the first quadrant, so we have only the red curve to consider, so that means working with tan(x) only. Again we want the radius of infinitesimally thin discs of thickness dx. The height of the red curve above the line y=a is tan(x)-a. This is the required radius. The limits for x involve the intersection of y=a with y=tan(x), that is, tan(x)=a or x=arctan(a) in radians. We want the volume of rotation around the line y=a so the limits for x are arctan(a) to π/2 and the integral is π∫(tan(x)-a)²dx.
c) When y=-5, 2-x³=-5, so x³=7 and x=1.9 approx. But the limit is x=π/2=1.6 approx, which means that x=1.9 is outside the designated limit. Also arctan(-5) is outside the first quadrant. There is no curve in the first quadrant so the volume is zero.
d) To rotate about the y-axis we can use horizontal infinitesimally thin discs so we use the integral π∫x²dy as the basis, and this time it’s the x coord that’s used for the radius. The equations are x=arctan(y) and x=∛(2-y).
I think that by now, you can see the method for finding these integrals. A picture does help a lot, and the one I’ve provided might be sufficient for you to answer the other parts to this question. Just take a close look at what the curves are doing in the region specified in the question.
In case you need to know, here are some integrals you may find useful.
π∫tan²(x)dx=π∫(sec²(x)-1)dx=π(tan(x)-x), which becomes a definite integral when the limits are applied.
π∫(2-x³)²dx=π∫(4-4x³+x⁶)dx=π(4x-x⁴+x⁷/7).
π∫(tan(x)-a)²dx=π∫(tan²(x)-2atan(x)+a²)dx=π(tan(x)-x+2aln(cos(x))+a²x).