Find the earliest interception and latest interception.

Question

My teacher wants us to solve this using excel. I'll leave out the extra stuff. "Your radar provides the following information about the incoming warhead at time of detection (t=0 seconds): vertical hight= 490,000 feet (about 93 miles) with an incoming vertical velocity= -4,107 feet/second. You know the following information about your Patriot missiles located at sea level: initial upwards velocity if 6,115 ft/second. You also know that each Chinese missile is typically designed to explode at 3 miles (about 16,000 feet) above the ground... armed with this information and using quadratic mathematics and MS Excel, answer the following questions: 1. If your missiles require a minimum of 10 seconds to launch from t=0, calculate the time and altitude of earliest interception. 2. What is the latest time (as measured from t=0) that you can launch the Patriots and still expect to intercept the missile...?" He wants us to put everything, including graphs, in a word document with the answers to the questions. I'd like to know how to get the functions to enter into excel. The early and late Patriot launches are confusing...

Answer 1

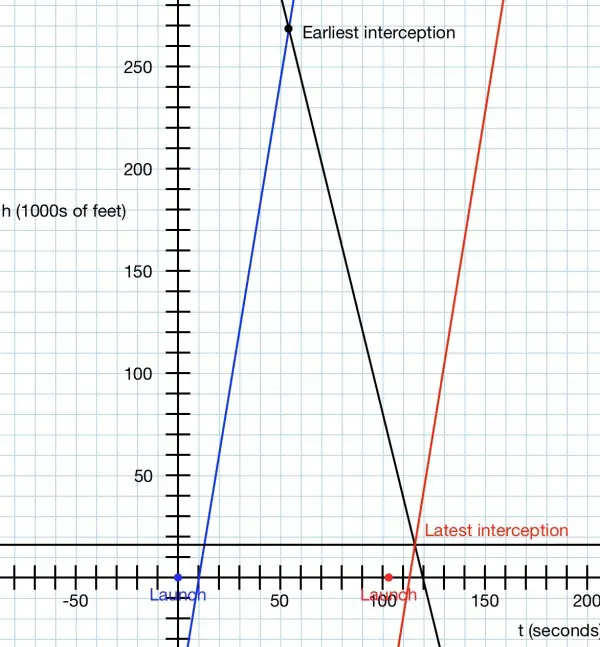
The mathematical equation for the warhead's height after time t seconds is h=490000-4107t. At t=0, h=490000.

The intercepting missiles are delayed by 10 seconds so the equation for their height is h=6115(t-10) so that when t=10, h=0. The warheads and interceptors are assumed to moving at uniform velocity, so graphically the height equations for both missiles are straight lines. Where they cross represents interception, which must take place before the warheads explode at h=16000. t=(490000-16000)/4107=115.41secs.

To find out the earliest time for interception we have 6115(t-10)=490000-4107t, when the missile and interceptor are at the same height. 6115t-61150=490000-4107t; 10222t=551150, t=53.92 secs. (h=268,550.56 ft approx.)

The latest time for interception is t=115.41 secs when the missiles explode. To reach a height of 16000 feet it takes the interceptor 16000/6115=2.62 seconds. Add on the 10 seconds to launch=12.62 secs. It takes the missile 115.41 secs to reach 16000 feet so the interceptor must be launched no later than t=115.41-12.62=102.79 seconds.

To illustrate this using Excel we could draw the two graphs initially, h being the vertical axis and t the horizontal: h=490000-4107t and h=6115(t-10). This represents the earliest time of interception. Then we need to "slide" h=6115(t-10) to the right to cross the other graph where h=16000. Where this shifted graph intercepts the t axis should correspond to 102.79 seconds. Some scaling down will be necessary for h perhaps measuring height in 1000's or 10000's of feet. The t axis should be scaled to accommodate about 120 seconds and of course the origin is on the extreme left.

If a graph is not used, Excel formula should be used to create a table of h and t values suitably spaced.

=IF(A1<10,0,6115*(A1-10)) can be used as a formula for the interceptor.

=IF(490000-4107*A1<16000,16000,490000-4107*A1) can be used as a formula for the missile. The graph can be inserted using the tabulated data.

Cell A1 contains t, so column A contains all the values of t you want to use. B1 and C1 correspondingly contain data for h for the two lines.