Quadrilaterals with the same perimeter lengths do not necessarily have the same area, so an angle between two sides is necessary to establish a specific area. The order of the sides is also necessary.
No angles or other information have been provided so the diagram below shows one possible quadrilateral:
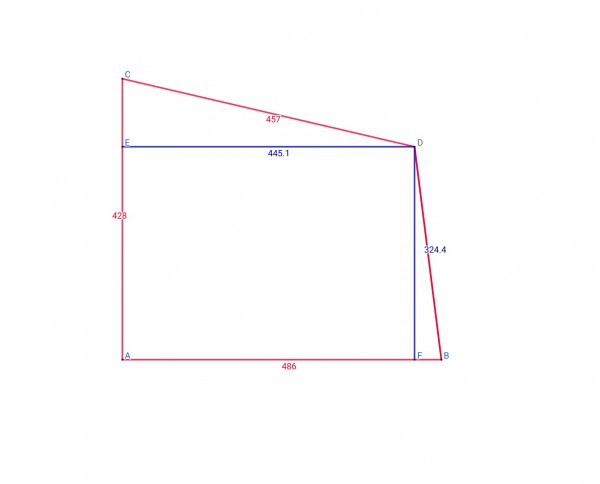
Note that AC=428' and AB=486' form a right angle. CD=457' and BD=327', which define the point D. The arithmetic for calculating D is complicated and is not shown here.
The total area (square footage)=area of rectangle EDFA+area of triangle CDE+area of triangle BDF.
Note that DE=AF and AE=DF, CE=AC-AE, BF=AB-AF
Area=DE.AE+½DE.CE+½DF.BF
Area=445.1×324.4+½(445.1(428-324.4)+324.4(486-445.1)),
Area=144390.44+½(23056.18+13267.96)=162,552.51 square feet.
This is only one possible solution out of many, but assuming an almost square configuration of sides, other solutions should give similar sized areas. For example, if AC and CD form a right angle the area would be 176,319.45 square feet. In this solution I assumed two sides were perpendicular, but the majority of quadrilaterals with the given side lengths will contain no right angles.