Two adjacent corrals are to be made using 240 ft of fencing.
The fence must around the outer perimeter and across the middle.
Find the dimensions so that the total enclosed area is as possible.
The picture is a rectangle. The fwnce is across the middle of the
rectangle. One side=y. The other side = x+x=2x. How do you know what
variable to solve for first and how do you determine the domain? Thanks.
You supplied no picture, but it's easy to draw one and solve the problem.
Use two horizontal fences and three vertical fences, as shown in the
picture I have below.
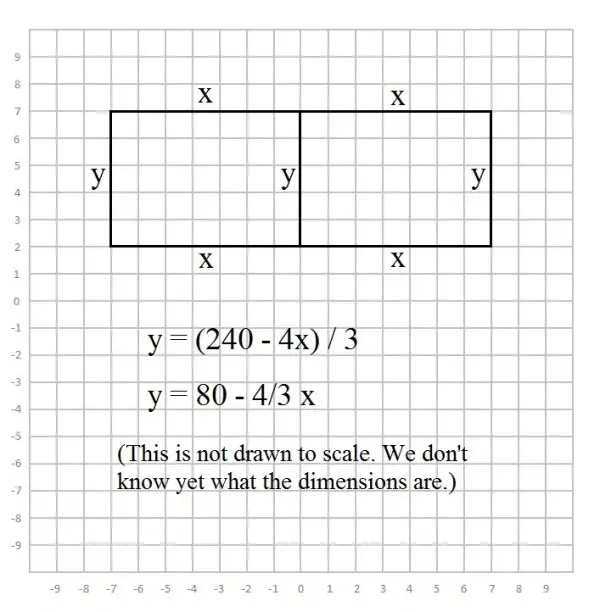
As you can see, the area of one of the smaller corrals is x * y. By
substituting the value of y in terms of x, we get x(80 - 4/3 x). Write
this as an equation.
y = x(80 - 4/3 x)
y = 80x - 4/3 x^2
Set this equal to zero to simplify dealing with the left side of the equation.
We will be working out the value of x where this graph crosses the x-axis,
so y is naturally zero.
0 = 80x - 4/3 x^2
Divide by -4/3.
0 = -60x + x^2
x^2 - 60x = 0
Complete the square. Add (1/2 * -60)^2 to both sides of the equation.
x^2 - 60x - 30^2 = 900 <<< that's -30 * -30
Factor the left side.
(x - 30)(x - 30) = 900
Take the square root of both sides.
x - 30 = ± 30
x = +30 + 30 and x = - 30 + 30
x = 60 and x = 0
This tells us that the graph of the equation is a parabola that
crosses the x-axis at (0, 0) and (60, 0). The vertex, which is
the highest point of the graph, is mid-way between those two points.
The value of x at that point produces the maximum area for the
smaller corral. Now, we calculate the value of y, using the formula
derived in the picture.
y = 80 - 4/3 x
y = 80 - 4/3 (30)
y = 80 - 4 (10)
y = 80 - 40
y = 40
The two smaller corrals are 30 x 40; the large corral is 60 x 40
The corresponding areas are 1200 (for each of the two smaller corrals)
and 2400 (for the large corral).
The length of the fencing is 4 * 30 + 3 * 40 = 120 + 120 = 240.
Now that we have the dimensions, we can see that the y sides are
longer than the x sides, but the picture served its purpose.