I read the equation as √(x/a)+√(y/b)+√(z/c)=1
√(z/c)=1-√(y/b)-√(x/a) and z/c=(1-√(y/b)-√(x/a))^2.
If we consider a cuboid (rectangular prism) of height z and length and width dx and dy, then the volume of the cuboid is zdxdy. The double integral will be ∫∫zdxdxy, representing the sum of an infinite number of cuboids with an infinitesimal cross-section, is the volume of the required solid. In this double integral we replace z by c((1-√(y/b)-√(x/a))^2). Now we need to work out the limits.
The positive square roots are implied.
Put z=0 into the equation. What we get is the x-y plane and a view of the end face of the solid. The curve meets the y-axis at (0,b) and the y-axis at (a,0). These are the y and x intercepts. Therefore we have the x and y limits for the double integral. For z>0 (up to z=c) we have laminae building up from the x-y plane. The area of one infinitesimally thin lamina is the area under the curve bounded by the intercepts. The sum of the laminae is the volume of the required solid. When z=c we reach the limit of the solid.
The question does not ask for evaluation of the double integral, but the process is to integrate c((1-√(y/b)-√(x/a))^2) wrt x treating y as a constant, between the limits x=0 and x=a; then the result is integrated wrt y between the limits y=0 and y=b. The limit of z=c isn't used because the equation defining z has been used as the integrand.
The answer is c∫∫((1-√(y/b)-√(x/a))^2)dxdxy with 0≤x≤a and 0≤y≤b.
The picture below shows in "net" form the general shape of the solid as folded-down axes to produce a 2-dimensional impression. By folding up the axes so that they form a 3-dimensional set of axes it's possible to imagine what the solid looks like:
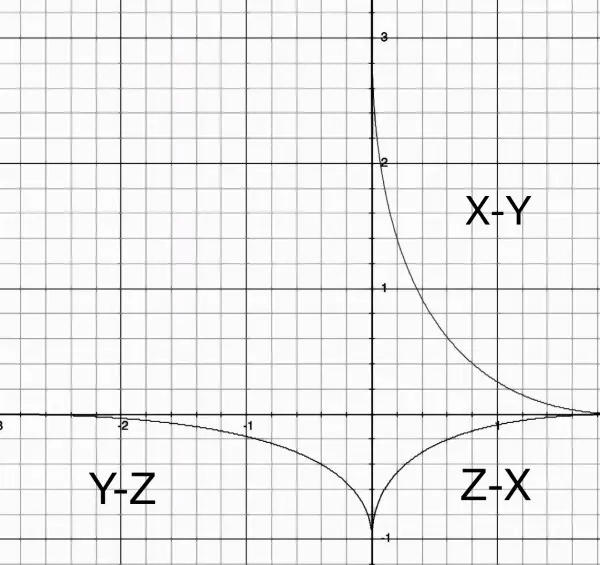
With Z-X as the base plane fold up Y-Z and X-Y so that the markers -2 and -1 in Y-Z are "stitched" to the markers 2 and 1 in X-Y making the X, Y and Z axes orthogonal like the corner of a cube. The result is a sort of cobweb strung across the corner, where the curves are the strands of the cobweb fastened to the "walls". Now mentally fill in the body of the cobweb, which is the required solid.