xy=4 means y=4/x so y'=-4/x^2. The slope of the normal is the negative reciprocal of this: x^2/4 at the point (x,4/x). 4x-y-2=0 is the same as y=4x-2. Lines parallel to this have the same slope, 4. So they are of the form y=4x+c where c is a constant. Therefore the slope of the normal and the parallel must be the same making x^2/4=4. So x^2=16 and x=4 or -4, corresponding to the normals at (4,1) and (-4,-1). Plug in these points and we have 1=16+c or -1=-16+c, making c=-15 or 15 respectively. So y=4x+15 or y=4x-15.
The picture below clearly shows the result.
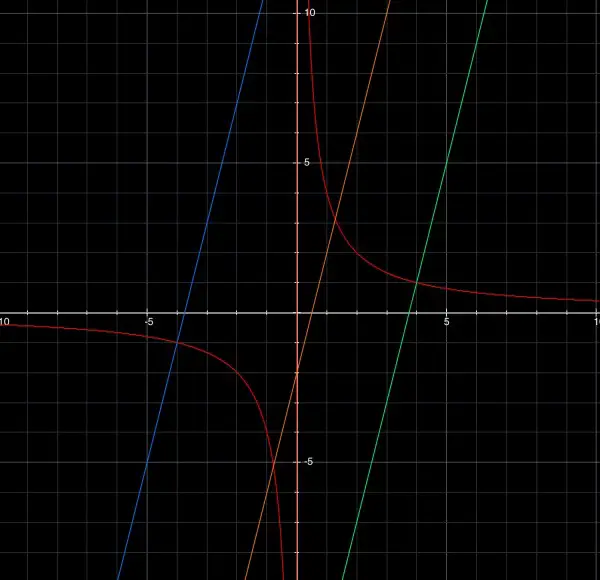
The red curve is xy=4; the brown line is 4x-y-2=0; and the blue and green lines are the normals. You can see the two points (4,1) and (-4,-1) where the normals intersect the curve.

