Question

Find an equation of the normal lines to the curve  = x^3 − 4x that is parallel to the line x + 8y –

8 = 0.

Answer 1

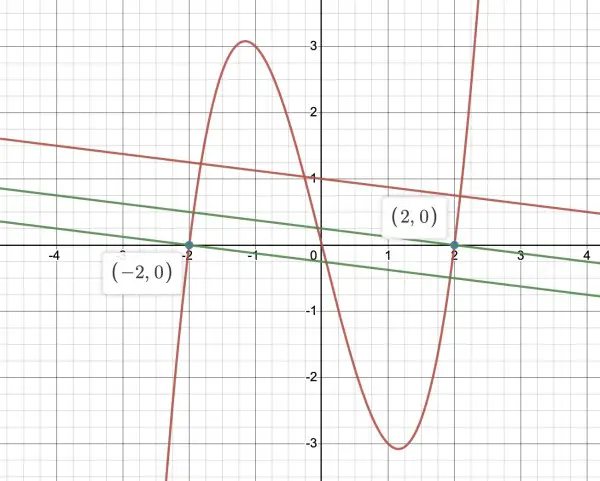
Let f(x)=x³-4x=x(x²-4), so df/dx=3x²-4 which represents the slope at the point (x,f(x)). The slope of the normal is the negative reciprocal of this slope=1/(4-3x²).

The line g(x)=x+8y-8 has slope  -⅛. To find out where 3x²-4 has the perpendicular (normal) slope -⅛ we need to find x in:

1/(4-3x²)=-1/8, that is, 4-3x²=-8, 3x²=12, x²=4, x=±2, f(±2)=±2(4-4)=0.

(We could also have solved 3x²-4=8, comparing the perpendicular of the line to the tangent of the curve.)

So the points are (2,0) and (-2,0).

The normal lines with slope -⅛ passing through each of these points are:

g(x)=⅛(2-x) and h(x)=-⅛(x+2). The picture shows the curve and line in red and the parallel normals in green.