on a coordinate grid what ordered pairs make a right triangle?

Question

a math question

Answer 1

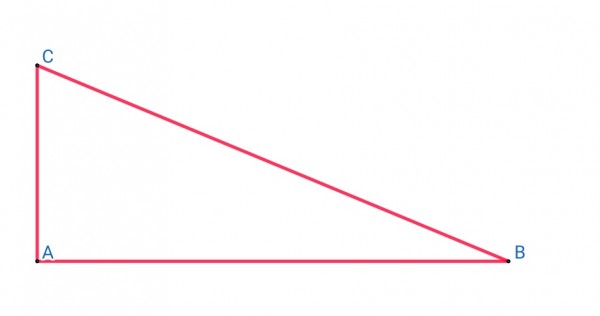
In the picture the triangle has the following coordinates A(0,0), B(b,0), C(0,c) where b and c are constants. All right triangles can be shown like this: put the right angle at the origin; b=AB in length, and c=AC in length. For example, b=12 and c=5. If A is moved from the origin to a point (h,k) then the coordinates become A(h,k), B(h+b,k), C(h,c+k). 

If the triangle is rotated clockwise (using A as a pivot) through an angle θ, the coordinates are transformed to A(h,k) unchanged, B(h+bcosθ,k-bsinθ), C(h+csinθ,k+ccosθ).