Function (x) = x^2 + px + q is 3 when x=-2 fubd valyes of p and q

Question

The least value of the function f (x) = x^2 + px + q is 3 and this occurs when x=-2 find values of p and q

It says: hence sketch the curve y=f (x), indicating all intersection pointd with the coordinates, then for part b it says find values of k in the equation below:

X^2 + (3k-7)x + (2k +6) =0 will have the real roots in x

Answer 1

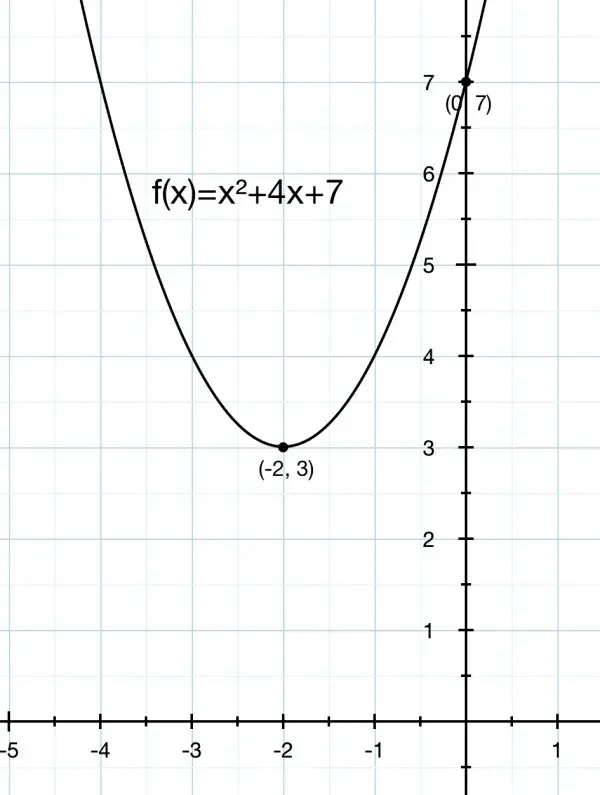
a) f(-2)=4-2p+q=3, so 2p-q=1. So f(x)=x²+px+2p-1.

The equation of the quadratic can be written y=(x-a)²+3, so it’s clear that the minimum value for y is when x=a. So y=x²-2ax+a²+3=x²+px+2p-1. And p=-2a and a²+3=2p-1, a²=2p-4. Substitute for a and we get:

p²/4-2p+4=0; p²-8p+16=0, (p-4)²=0, so p=4 and q=2p-1=7.

f(x)=x²+4x+7; f(-2)=4-8+7=3, so that fits the requirements.

 

b) x²+(3k-7)x+2k+6=0.

Complete the square: x²+(3k-7)x+(3k-7)²/4+2k+6=(3k-7)²/4.

(x+(3k-7)/2)²=-2k-6+(3k-7)²/4=

(-8k-24+9k²-42k+49)/4=(9k²-50k+25)/4=

(9k-5)(k-5)/4.

(9k-5)(k-5)/4≥0 for real roots. So k≥5 or k≤5/9 satisfies this condition.