find two vectors of norm 1 that are orthogonal to <3, -2>

Question

this is dealing with a point and finding 2 vectors normal to it and normal is length 1

Answer 1

The given vector can be represented by the line y=-2x/3 in Cartesian coordinates. The vector is the line segment between (0,0) and (3,-2). The normals can be represented by y=3x/2.

If the vector is represented by the line joining (0,0) to a point (p,q) then p²+q²=1, because the normal has length 1, and q=3p/2. So p²+9p²/4=1, 13p²/4=1, p=±√(4/13)=±2/√13, q=±3/√13. One normal vector is <2√13/13,3√13/13> after rationalisation and the other is <-2√13/13,-3√13/13>.

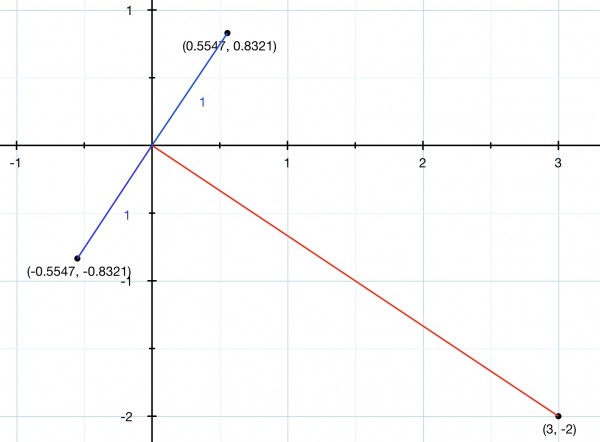
The red line represents the given vector and the blue lines represent the two normals. The irrationals are shown accurate to 4 places of decimals.