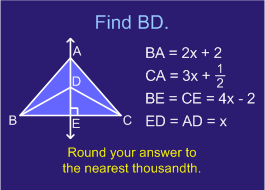
AE is perpendicular to BC.
BE = CE (given)
Since AE is a perpendicular of BC, and BE = CE, then AE is a perpendicular bisector of the triangle ABC.
Hence triangle ABC is isosceles and AB = AC.
Since AB = AC, then
2x + 2 = 3x + ½
x = 3/2
AC = 3x+ ½ = 9/2 + ½ = 5
AC = 5
EC = 4x – 2 = 6 – 3 = 4
EC = 4
Also, ED = x
ED = 3/2
Using Pythagoras’ Theorem,
BD^2 = BE^2 + ED^2
BD^2 = 4^2 + (3/2)^2 (using BE = EC = 4)
BD^2 = 16 + 9/4
BD^2 = 18.25
BD = √(18.25)
BD = 4.272