U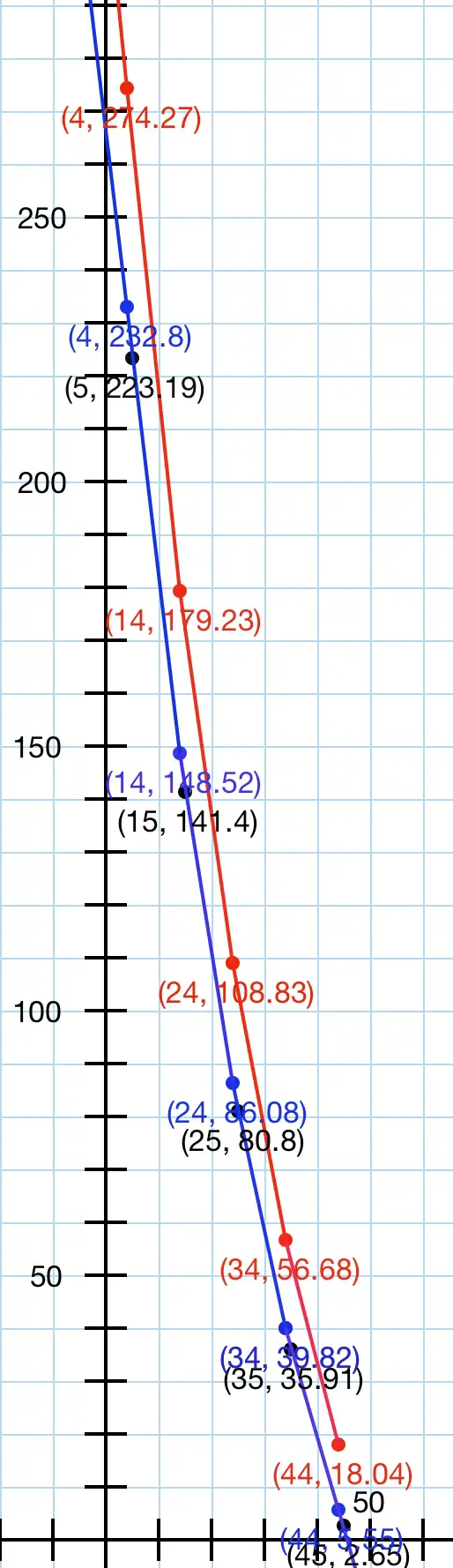
The graph above is intended to represent the given data, which seems to be incomplete or ambiguous. The red points and lines joining the points appear to represent what was meant to be Table I, and the blue points and lines Table II. The black points seem to be meaningful to the blue data, because the red data are to the right of them. I assume that you need answers with reference to the red Table I data.
The slopes of the lines are negative indicating deceleration, so acceleration will be shown as negative.
(i) We need to calculate the average slope between the lowest given data for t and the highest.
(4,274.27) is the earliest point and (44,18.04) the latest. The slope is (18.04-274.27)/(44-4)=-6.40575 (average acceleration). From this we can work out v-274.27=-6.40575(t-4), where v(t) is the function for the velocity. From this the function and equation for the average line is v(t)=-6.40575t+25.623+274.27. Therefore v(t)=-6.40575t+299.893. From this we see that the v intercept (initial velocity at t=0) is about 300ft/s. We already know that the average acceleration is -6.40575 ft/s².
(ii) The nearest t values are t=24 and t=44, so we calculate the slope from these coords: (24,108.83) and (44,18.04), (18.04-108.83)/20=-4.5395. So the average acceleration over this time period is -4.5395ft/s².
(iii) We need to interpolate because there is no point close enough for t=40, so we pick t=39 which is midway between 34 and 44 and we arrive at (39,37.36) because 37.36=(56.68+18.04)/2. Over the 5 second interval then we have a slope of (18.04-37.36)/5=-3.864 ft/s².