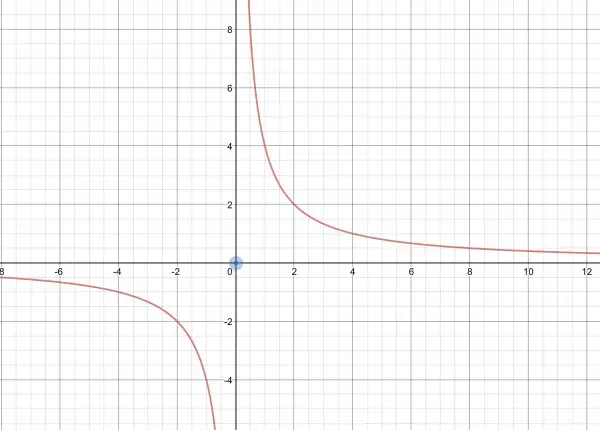
First, the given equation is a hyperbola in the x-y plane as shown by the red lines. Imagine you are looking down the z-axis (rising at right angles from the bluish point at the x-y origin in the x-y plane. The hyperbola is extruded into the z direction, so the picture shows a cross-section of the hyperbolic cylinder(s). The red lines show the vertical “walls” of two cylinders. However, the “cylinders” have walls extending to infinity so their circumferences are infinite. And of course the cylinders are infinitely tall because the z-axis is infinitely long.