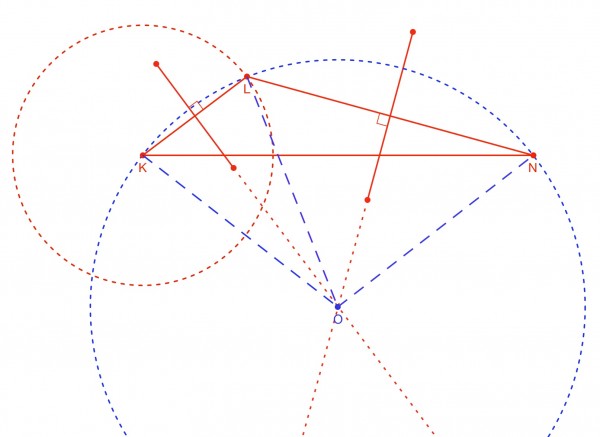
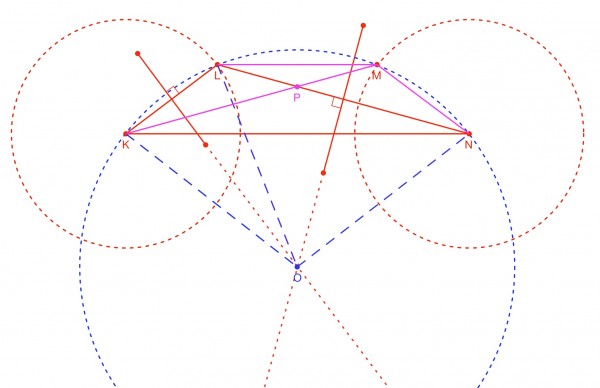
The top picture shows a triangle KLN, the perpendicular bisectors of KL and LN and their intersection at O, which is the centre of the circumcircle for triangle KLN. Note that this construction creates two isosceles triangles (equal sides shown by dashed blue lines). All triangles have a circumcircle, so K, L and N are concyclic. The circle with centre at K represents all points equidistant from K. In other words the circumference is the locus of all points for L. A similar circle has been drawn at point N, so the circumference is the locus of all point for M. And the sides KL and MN are equal (given). (The radii (KO, LO, MO (not shown), NO) are of course equal.) This creates a symmetry which forces LM to be parallel to KN. KLMN is a trapezoid (trapezium) (see lower picture). Now consider the point M being anywhere else except where it is shown. (It would still need to lie on the circle drawn around N.) If this were the case, angle KLM could not be equal to angle LMN, because LM and KN would not be parallel and the component angles of KLM could not be equal to the component angles of LMN. Therefore M must lie on the circumcircle, making all the vertices of KLMN concyclic.
Points to note include:
Chord KL subtends two equal angles: ∠LMK=∠LNK
Similarly, chord MN subtends two equal angles: ∠MKN=∠MLN
Chord KN subtends two equal angles: ∠KLN=∠KMN
By symmetry, because MN=KL, all four angles are equal
Alternate equal angles on a transversal prove that KL and MN are parallel


The top picture shows a triangle KLN, the perpendicular bisectors of KL and LN and their intersection at O, which is the centre of the circumcircle for triangle KLN. All triangles have a circumcircle, so K, L and N are concyclic. The circle with centre at K represents all points equidistant from K. In other words the circumference is the locus of all points for L. A similar circle has been drawn at point N, so the circumference is the locus of all point for M. And the radii KL and MN are equal (given). This creates a symmetry which forces LM to be parallel to KN. KLMN is a trapezoid (trapezium) (see lower picture). Now consider the point M being anywhere else except where it is shown. It would still need to lie on the circle drawn around N. If this were the case, angle KLM could not be equal to angle LMN, because LM and KN would not be parallel and the component angles of KLM could not be equal to the component angles of LMN. Therefore M must lie on the circumcircle, making the vertices of KLMN
Points to note include:
Chord KL subtends two equal angles: ∠LMK=∠LNK
Similarly, chord MN subtends two equal angles: ∠MKN=∠MLN
Chord KN subtends two equal angles: ∠KLN=∠KMN
By symmetry, because MN=KL, all four angles are equal
Alternate equal angles on a transversal prove that KL and MN are parallel
Triangles KLN and KMN are congruent and isosceles triangles LPM and KPN are similar
Component angles ∠KLM=∠KLN+∠NLM=∠LMN=∠LMK+∠KMN