Question

The graph of a parabola passes through the points (3/2, 4/3) and (0, −6) and has a horizontal tangent line at (3/2, 4/3). Find an equation for the parabola and sketch its graph.

Answer 1

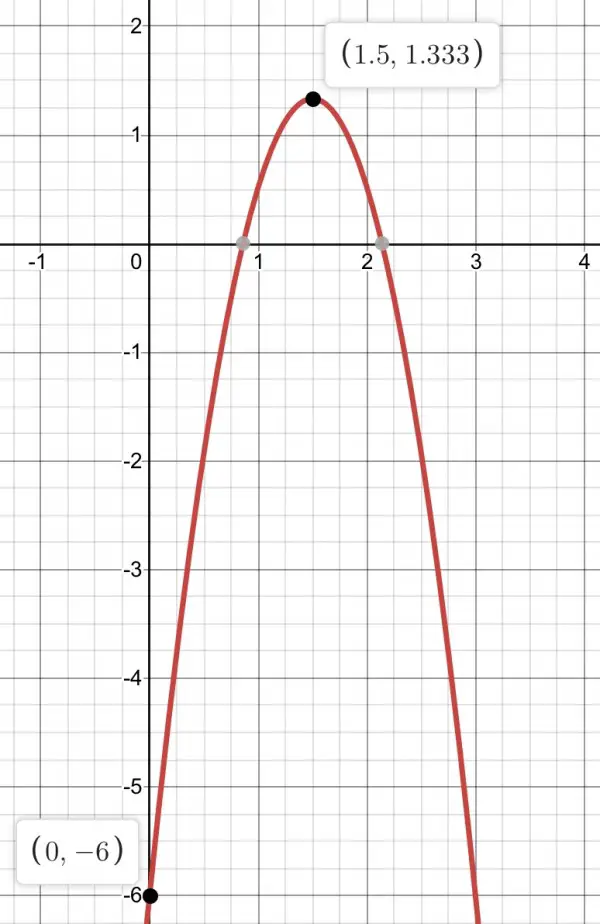
In general form the equation of a parabola is quadratic:

y=ax²+bx+c, where a, b, c are constants to be found.

We plug in the given points:

4/3=9a/4+3b/2+c, -6=c, y=ax²+bx-6 and 4/3=9a/4+3b/2-6. Still have to find a and b.

dy/dx=2ax+b=0 (horizontal) at x=3/2, so 3a+b=0, making b=-3a, which we can substitute in 4/3=9a/4+3b/2-6.

4/3=9a/4-9a/2-6, 4/3+6=-9a/4, 22/3=-9a/4, a=-(4/9)(22/3)=-88/27. Therefore b=88/9.

y=-88x²/27+88x/9-6 is the equation of the parabola.