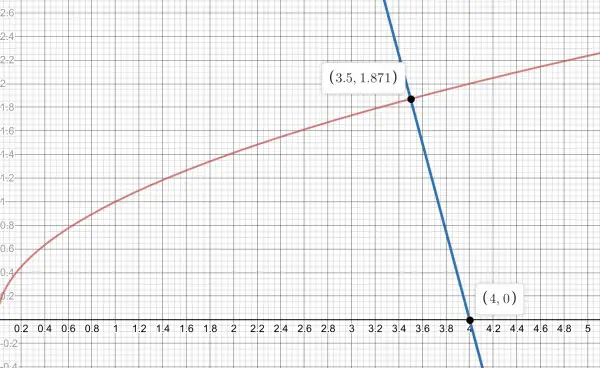
The shortest distance L from (4,0) is a radius to the tangent at (4,0).
dy/dx=1/(2√x). This is at the point (x,√x). The gradient at right angles to this is -2√x the slope of the radius L. If the point on the curve is (a,√a), the gradient of the radius is -2√a.
The equation of the radius is y=-2√a(x-4) because the radius passes through the point (4,0). We don’t know a yet but we do know that y=√a, the curve, and the intersection is √a=-2√a(x-4), 1=-2(x-4), 1=-2x+8, 2x=7, x=3.5. So the point of intersection is (3.5,√3.5). To find the length L we use Pythagoras: L²=(4-3.5)²+3.5=0.25+3.5=3.75, L=1.94 approx.
The graph below shows the radius intersecting the curve: