Plug in x=1:
1+(y-1)³=9, (y-1)³=8, y-1=2, y=3. The graph passes through (1,3).
Differentiate x²+(y-x)³=9=x²+y³-3xy²+3x²y-x³ wrt x:
2x+3y²dy/dx-6xydy/dx-3y²+3x²dy/dx+6xy-3x²=0,
2x+dy/dx(3y²-6xy+3x²)-3y²+6xy-3x²=0,
3(y-x)²dy/dx=3(y-x)²-2x,
dy/dx=(3(y-x)²-2x)/(3(y-x)²) or 1-2x/(3(y-x)²)
Plug in (1,3): dy/dx=1-2/(3(3-1)²)=1-⅙, and dy/dx=5/6, the slope of the tangent line.
The equation of the line at (1,3) is y-3=(5/6)(x-1), y=3+5x/6-5/6=5x/6+13/6.
The graph below shows this tangent line and seems to confirm the solution y=5x/6+13/6:
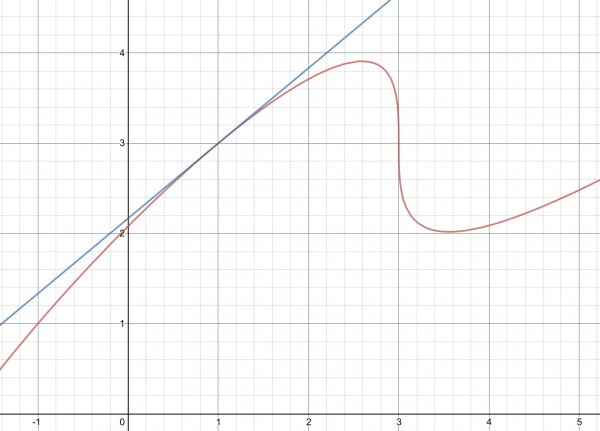
None of the answer options can be correct because none pass through the tangent (1,3).