A sheet of cardboard 3 ft. by 4 ft. will be made into a box by cutting equal-sized squares from each corner and folding up the four edges.

Question

Given that variable x shall be the length of one edge of the square cu from each corner of the sheet of cardboardwhat will be the dimensions of the box with largest volume?

Given that variable x shall be the length of one edge of the square cu from each corner of the sheet of cardboard, what will be the dimensions of the box with largest volume?

Given that variable x shall be the length of one edge of the square cu from each corner of the sheet of cardboard, what will be the dimensions of the box with largest volume?



 

Answer 1

Volume V=x(4-2x)(3-2x)=12x-14x²+4x³

dV/dx=12-28x+12x²=0=3-7x+3x², x=(7±√(49-36))/6=(7±√13)/6=1.768 or 0.567.

The quantity 3-2x is negative when x=1.768 so, since the volume is positive, x=0.567 feet.

The dimensions are 4-2x=2.8685, 3-2x=1.8685, x=0.5657 feet. Volume=3.0323 cubic feet.

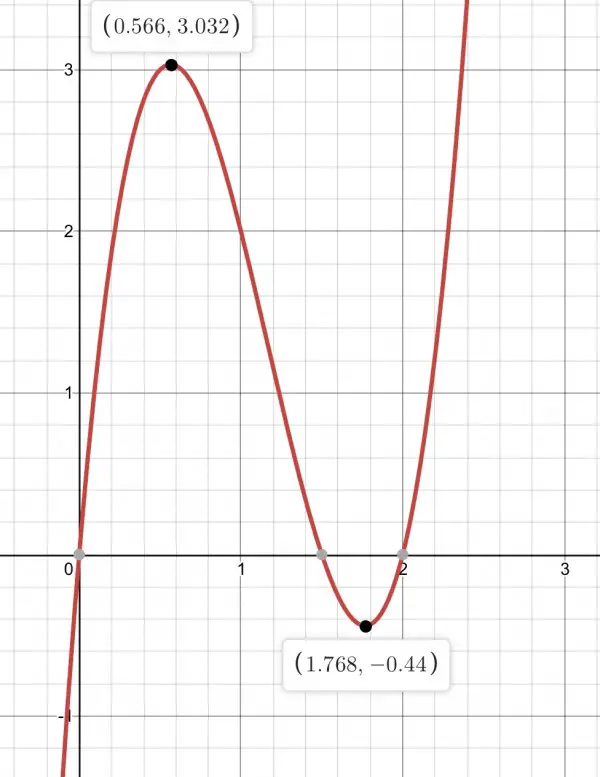
The graph shows the volume (vertical axis) for varying values of the depth x.

 

Answer 2

Парсер гугла без проблем. Видео смотрите сами