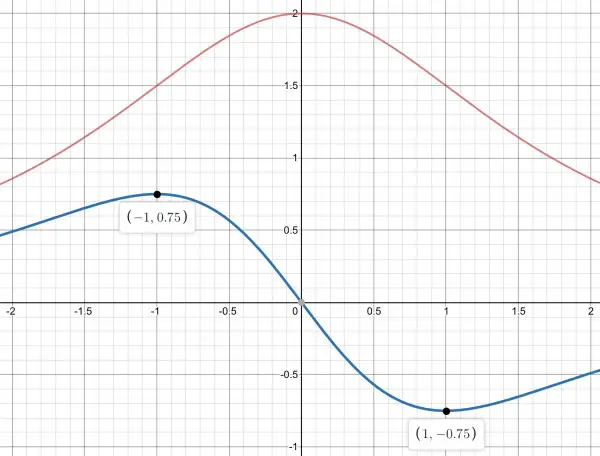
First we need to find the gradient, S=y'=-12x/(x²+3)². This gives us the gradient or tangent for all values of x. For example, the tangent is zero at x=0 (y=2), at (0,2). We need to find the minimum gradient (e.g., <0) and maximum (e.g., >0). We need to differentiate again: y''=48x²/(x²+3)³-12/(x²+3)². When this is zero we get the value of x for max and min gradients. Solve 48x²/(x²+3)³-12/(x²+3)²=0, 48x²/(x²+3)³=12/(x²+3)², 4x²/(x²+3)=1, 4x²=x²+3, 3x²=3, x=±1. So let’s work out S=y'=-12/16=-¾ at x=1 and S=12/16=¾ at x=-1. So:
Smallest slope is -¾ at (1,3/2) and largest ¾ at (-1,3/2).
Largest: x=-1, y=1.5, S=0.75; smallest: x=1, y=1.5, S=-0.75.