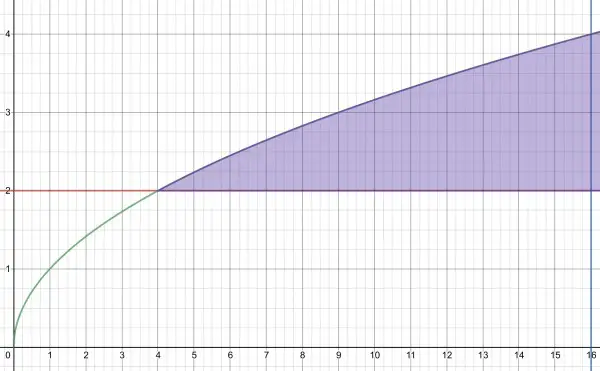
The shaded area to the left of the vertical blue line x=16 is rotated around the horizontal red line y=2. The green curve is y=√x (assumed from the question).
This shape is to be rotated around the horizontal line y=2. Consider the shaded area as divided into narrow strips of width dx. The height r of each strip can be calculated from its x coordinate. Note that the lowest value of x is 4, where y=2 intersects y=√x, that is, 2=√x, 4=x. r=√x-2, which is the point (x,√x) with reference to the line y=2, and is the radius of the strip to be rotated. When the strip is rotated around the spindle y=2 it becomes a disc with volume πr²dx=π(√x-2)²dx. So the volume of the solid is the sum of all strips between x=4 and x=16. This sum is ∫π(√x-2)²dx for the interval x ∊ [4,16].
Volume is therefore π∫(x-4√x+4)dx=π(x²/2-(8/3)√x³+4x)[4,16]=
π(128-512/3+64-8+64/3-16)=56π/3 cubic units.