Here is the graph:
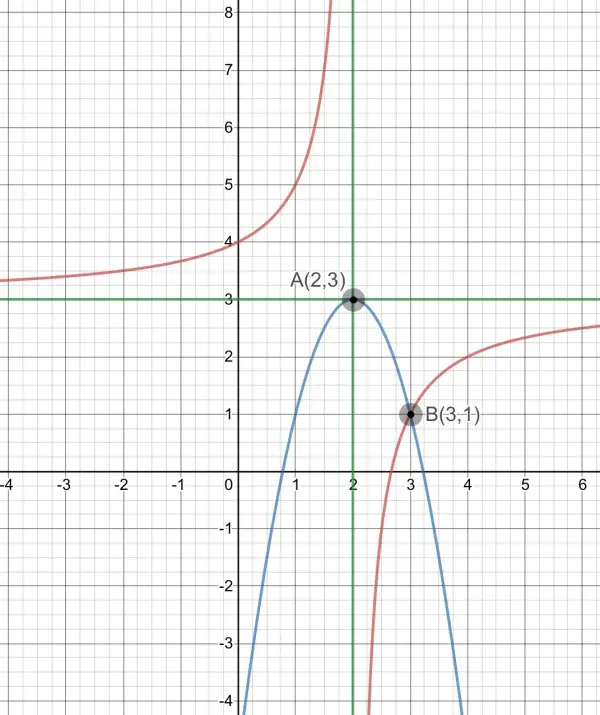
The points A and B are shown, as well as the hyperbola (red) and its asymptotes (green), and the parabola (blue).
(1) Asymptotes are x=2 and y=3 (rectangular hyperbola). The reason is as follows. Let y=h(x), then y-q=a/(x-p), so we can also write x-p=a/(y-q). Suppose x is very large then a/(x-p) gets very small until it’s almost zero, so y-q→0, or y→q, which is an asymptote. Similarly, since x-p=a/(y-q), x→p when y is very large. So the asymptotes are y=q and x=p, and they intersect at A(p,q)=(2,3), making p=2 and q=3. h(x)=a/(x-2)+3. To find a we need part (2):
(2), (3) and (4) Point B must be on both the hyperbola and the parabola, so h(3)=1, 1=a/(3-2)+3, a=-2 and h(x)=-2/(x-2)+3. We also know that the vertex of the parabola is at A, so the equation of the parabola has the form y-3=b(x-2)² where b is a constant. Point B is on the parabola, so 1-3=b(3-2)², -2=b, and the equation of the parabola is y-3=-2(x-2)². From this, y=-2(x²-4x+4)+3, p(x)=y=-2x²+8x-5.
(5) Algebraically h(x)=p(x) when the curves intersect:
-2/(x-2)+3=-2(x-2)²+3
-2/(x-2)=-2(x-2)², then, divide each side by -2:
1/(x-2)=(x-2)²,
(x-2)³=1, so, taking the cube root of each side:
x-2=1, x=3. Now find p(3) or h(3) = 1.
So B(3,1) is the only point of intersection.