All measurements are in cm.
[Let y=AB, x=CD, ∠BAD=θ=∠DAC, AC=12 and BD=4.
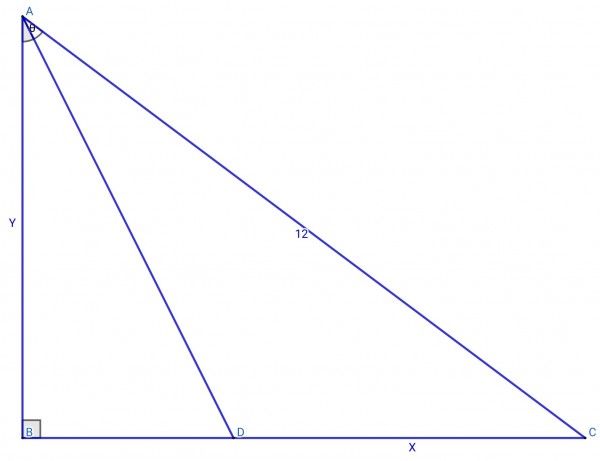
Area of ADC=½xy, (x+4)²+y²=144, so y²=144-(x+4)²=128-x²-8x.
tanθ=4/y, tan(2θ)=(x+4)/y=2tanθ/(1-tan²θ)=8y/(y²-16).
Assume y≠4, because this would cause division by zero.
So (x+4)/y=8y/(y²-16),
(x+4)(y²-16)=8y²,
xy²-16x-4y²-64=0,
y²(x-4)=16(x+4), y²=16(x+4)/(x-4).
So we have two expressions for y², therefore:
16(x+4)/(x-4)=128-x²-8x,
16x+64=128x-x³-8x²-512+4x²+32x,
x³+4x²-144x+576=0, which has no positive real solutions.
Therefore, the above interpretation of the figure cannot be correct. The problem in attempting to apply this solution is that BD at 4cm is too long; the maximum length for a solution requires BD to be about 3.6cm.]
The figure below fits the requirements and has a solution.
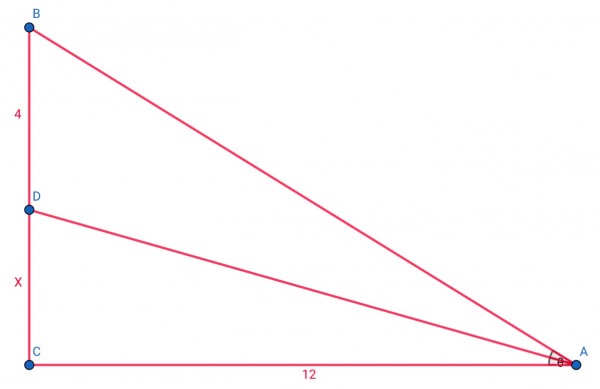
Let x=CD, θ=∠DAC=∠BAD, AC=12, BD=4.
tanθ=x/12, tan(2θ)=(x+4)/12,
but tan(2θ)=2tanθ/(1-tan²θ)=(x/6)/(1-x²/144),
(x+4)/12=(x/6)/(1-x²/144)=24x/(144-x²),
(x+4)(144-x²)=288x,
144x-x³+576-4x²=288x,
x³+4x²+144x-576=0. Let f(x)=x³+4x²+144x-576.
This cubic has a positive root. Use Newton’s Method to solve, starting with x₀=3.
xᵢ₊₁=xᵢ-f(xᵢ)/f'(xᵢ) is the iteration formula.
x₁=3.4153...
x₂=3.4041...
Final solution is x=3.4042cm approx.
Area of ∆ADC=6x=20.4249 sq cm approx. Using AC=12 as the base of ∆ADC.
There may be other solutions depending on interpretation of the figure.