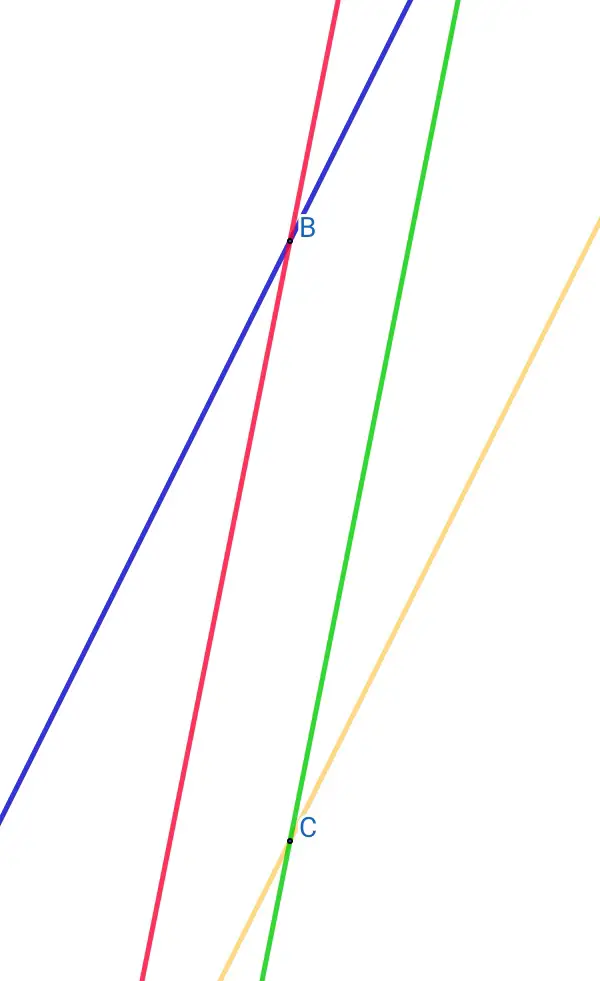
To make an angle we need two lines that are not parallel, so that they intersect.
Let B be the intersection point.
Next we draw a green line parallel to the red line and an orange line parallel to the blue line. They intersect at C.
At the intersection point B there are 4 angles,—two pairs of equal angles. Label the 4 angles clockwise B1, B2, B3, B4, where B1 is the topmost acute angle. Similarly at point C. The green and red lines are parallel, as are the blue and orange lines, so at C there are also 4 angles, labelled similarly C1, C2, C3, C4.
|
m∠B1=m∠B3
|
Opposite angles at an intersection.
|
|
m∠B2=m∠B4
|
Opposite angles at an intersection.
|
|
m∠C1=m∠C3
|
Opposite angles at an intersection.
|
|
m∠C2=m∠C4
|
Opposite angles at an intersection.
|
|
m∠B1=m∠C1, m∠B2=m∠C2, m∠B3=m∠C3, m∠B4=m∠C4.
|
Corresponding angles on parallel lines.
|
|
Slide point C onto point B.
|
Translation.
|
|
All 4 angles at C coincide with the 4 angles at B.
|
This coincidence is called congruency.
|
|
Rotate the green and orange lines about the point C so that the lines are superimposed and ∠B1 is exactly superimposed by ∠C3, ∠B2 by ∠C4, ∠B3 by ∠C1, ∠B4 by ∠C2.
|
The superposition makes ∠B1 and ∠C3, ∠B2 and ∠C4, ∠B3 and ∠C1, ∠B4 and ∠C2 congruent.
|
|
Therefore:
|
Angles B and C are congruent.
|