I think we need to be careful about this problem, because some of the enclosed area comes below the x-axis which would give us a negative value for this part of the area. First we need to find the intersection points: y=x3-6x2+8x=x2-4x. Since x=0 is a solution (0,0) is one intersection.
x2-6x+8=x-4, x2-7x+12=(x-3)(x-4) so (3,-3) and (4,0) are the other intersections. (When x=3, y=x2-4=9-12=-3; when x=4, y=16-16=0.)
A rough sketch of the graph at this stage is helpful.
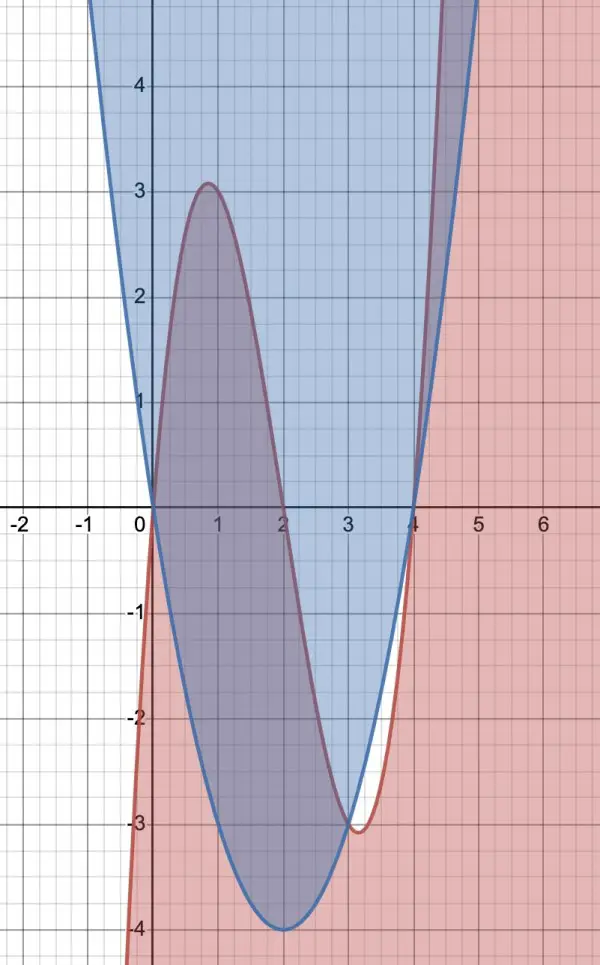
The dark shaded area is what we want. The thin dark shaded area to the right is not bounded so we can ignore that---because we only need the enclosed area. The area between x=2 and x=3 is entirely below the x-axis. Let's see what it is using ydx as the integrand. y is the difference between the two functions. In this region, the cubic is above the quadratic so y=x3-6x2+8x-(x2-4x)=x3-6x2+8x-x2+4x=x3-7x2+12x.
2∫3ydx=2∫3(x3-7x2+12x)dx=[x4/4-7x3/3+6x2]23=(81/4-63+54)-(4-56/3+24)=45/4-28/3=23/12.
Between x=0 and x=2 the cubic is still above the quadratic so:
0∫2ydx=[x4/4-7x3/3+6x2]02=28/3. The total area is therefore 28/3+23/12=45/4 square units.
This is the same result as applying the limits [0,3], but it's always wise to check what's going on when dealing with areas that may include those in the negative regions.