sample a starts with 200,000 bacteria. the population doubles every hour. write an exponential functions that models the population in sample a as a function of time in hours

Question

Scientists are growing bacteria in a laboratory. They start with a known population of bacteria and measure how long it takes this population to double.

5. Sample A starts with 200,000 bacteria. The population doubles every hour. Write an exponential function that models the population in Sample A as a function of time in hours

6. Sample B starts with 50,000 bacteria. The population doubles every half hour. Write an exponential function that models the population growth in Sample B as a function of time in hours.

7. Write an inequality that models the population in Sample B overtaking the population in Sample A.

8. Use a graphing calculator to solve the inequality.

Answer 1

(Q5) General exponential equation P(t)=P₀e^kt where P₀ is the initial population when t=0, where t is the number of hours and k is a constant. P is the population after time t hours.

P₀=200000. When t=1 (hour), the A population doubles, so P_A(1)=400000=200000e^k, e^k=2, k=ln(2), so P_A(t)=200000e^tln(2).

P_A(t)=200000(2^t) because tln(2)=ln(2^t).

(Q6) P_B(t)=50000(4^t), because after an hour P_B doubles twice and 2²=4. This can also be written:

P_B(t)=50000(2^2t). (When t=½, P_B(½)=100000; 4^t=4½=√4=2; 2^2t=2¹=2.)

(Q7) Inequality is P_B>P_A, that is: 50000(2^2t)>200000(2^t), 2^2t>4(2^t), 2^2t>2²(2^t), 2^2t>2^t+2, 2t>t+2, t>2 is the inequality, meaning that (Q8) t is more than 2 hours. (Example: t=2½ hours: P_B=1,600,000; P_A=1,131,370.)

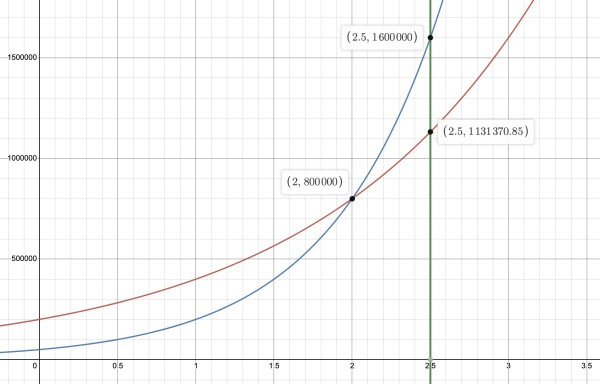
P_A is shown in red while P_B is in blue. The green line represents t=2.5 hours. The blue curve is higher than the red when t>2 hours.