(The question doesn't state where S and T are positioned, hence the following assumption and argument.)
I figured that, since S is NM produced, something must fix the position of S. I'm guessing it's to form the rectangle TLSN, where, by symmetry, T is LK produced. If this is the case, P is also the intersection of the diagonals of TLSN, and is the midpoint of the height of KLMN and TLSN which have the same height, by construction. This height is given by TN, and if Q is its midpoint, then QP is parallel to KL and NM. PQ is also perpendicular to TN.
But TQ=QN because Q is the midpoint of TN. TPN is therefore an isosceles triangle because the perpendicular from the apex angle TP̂N on to the base TN bisects the base (TQ=QN). Therefore NP=PT (the two equal sides) and their ratio is NP:PT=1.
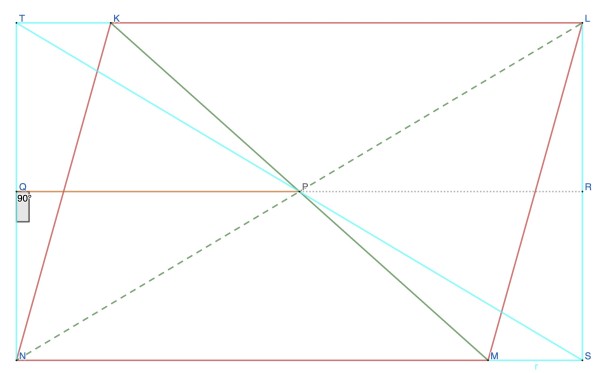
The picture shows the parallelogram KLMN (red) embedded in the rectangle TLSN with diagonal TS (construction lines shown in cyan). The diagonals (of the parallelogram) KM and NL are shown in green, with diagonal NL common to KLMN and TLSN shown in dashed green. PQ (orange) is shown to be perpendicular to TN with right angle at Q. QP is extended to R and so PR (faint dotted line) is perpendicular to LS (this fact is not used in the solution). The picture is based on the assumptions made earlier.
[Acknowledgments to GeoGebra Calculator Suite for the tools to create the picture.]