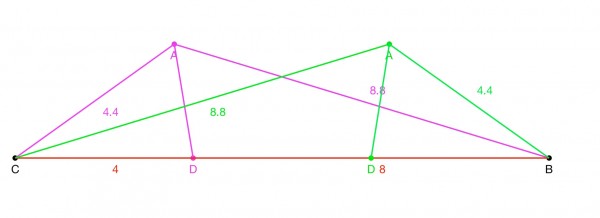
In the pink triangle ABC, the bisector of angle A meets BC at D. Let AC=4.4, CD=4 and BD=8, so BC=12. We have to find AB.
Let ∠CAD=∠DAB=x and ∠ACD=y.
We can apply the Sine Rule to the three triangles ACD, ABC and ABD:
ACD: 4.4/sin(x+y)=AD/sin(y)=4/sin(x)=p the common ratio.
ABC: 12/sin(2x)=AB/sin(y)=4.4/sin(2x+y)=q the common ratio.
ABD: AD/sin(2x+y)=AB/sin(x+y)=8/sin(x)=r the common ratio.
Note that the sine of the supplement of an angle is the same as the sine of the angle, that is, sin(θ)=sin(180-θ). Note also that, since 4/sin(x)=p and 8/sin(x)=r, r=2p. Therefore, AB/sin(x+y)=2×4.4/sin(x+y)=8.8/sin(x+y), making AB=8.8.
In this case the 4.4 side is adjacent to the segment with length 4. We need to examine the case when the 4.4 side is adjacent to the segment with length 8.
Here we have AC=4.4, but CD=8 and BD=4. We still need to find AB.
Applying the Sine Rule we get:
ACD: 4.4/sin(x+y)=AD/sin(y)=8/sin(x)=p the common ratio.
ABC: 12/sin(2x)=AB/sin(y)=4.4/sin(2x+y)=q the common ratio.
ABD: AD/sin(2x+y)=AB/sin(x+y)=4/sin(x)=r the common ratio.
Therefore, p=2r, 4.4/sin(x+y)=2AB/sin(x+y), so AB=2.2.
The Triangle Rule requires the sum of the lengths of any two sides to be greater than the length of the third side. We have AB=2.2, BC=12 and AC=4.4. But AB+AC=6.6, and this is shorter than BC. So the 4.4 side must be adjacent to the segment of length 4 to form a valid triangle. This leaves us with the length of the third side as 8.8. The picture shows two possible triangles (pink and green), but the length of the third side is 8.8 for each. In the green triangle we find AC has the same length as AB in the pink triangle because of symmetry and congruency.