Find (f^−1)'(a). f(x) = 4x3 + 3x2 + 6x + 7, a = 7

Question

finding the inverse function

Answer 1

f(x)=4x³+3x²+6x+7, f'(x)=6(2x²+x+1).

Let y=f'(x), then x=f'^-1(y), so if y=a, x=f'^-1(a), a=f'(x)=6(2x²+x+1),

2x²+x+1=⅙a,

x²+½x=a/12-½,

x²+½x+1/16=a/12-8/16+1/16=a/12-7/16,

(x+¼)²=(1/16)(4a/3-7),

x=±¼√(4a/3-7)-¼.

When a=7, x=±¼√(28/3-7)-¼,

x=±¼√(7/3)-¼.

Therefore, since x=f'^-1(a), f'^-1(a)=±¼√(7/3)-¼=(-3±√21)/12.

f'^-1(a)=(-3±√21)/12 (0.1319 or -0.6319 approx).

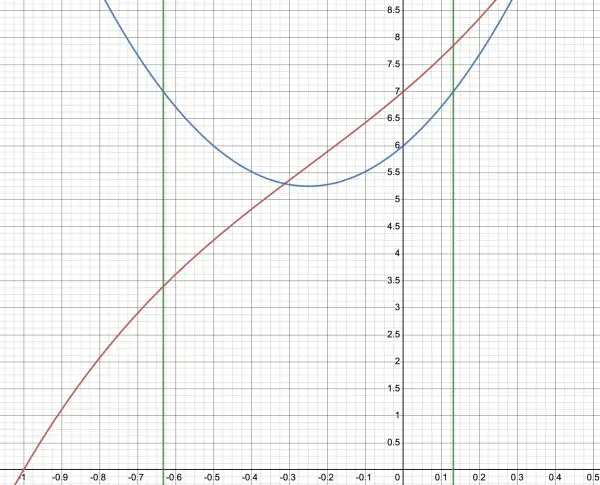
The graph in red represents part of f(x), while f'(x) is shown in blue.

The green verticals represent the two solutions for f'^-1(a) when a=7.

NOTE

If f^-1(a) had been required, let y=f(x), so x=f^-1(a) when y=a=7, then:

a=f(x)=4x³+3x²+6x+7,

4x³+3x²+6x+7-a=0, 4x³+3x²+6x=0 when a=7, x(4x²+3x+6)=0⇒x=0 because the quadratic has only complex solutions.

Therefore x=f^-1(a)=0 (one real solution).