First, we need to solve the DE, which can be rewritten: y'-2y=te^3t.
Multiply through by an unknown function f(t):
y'f(t)-2yf(t)=f(t)te^3t.
If we can find f(t) such that f'(t)=-2 then we can begin to integrate:
If f'=-2 then f=c-2t where c is a constant. This means that the left-hand side is d((c-2t)y)/dt.
So we can now integrate: (c-2t)y=∫((c-2t)te^3tdt)=∫(cte^3tdt)-∫(2t^2e^3tdt)=I-J. [Not sure whether this integration requires another constant of integration. Assume it doesn't.]
I=∫(cte^3tdt): let u=ct and dv=e^3tdt; du=cdt and v=e^3t/3.
d(uv)=vdu+udv; integrating: cte^3t/3=uv=∫(ce^3tdt/3)+I=ce^3t/9+I, so I=cte^3t/3-ce^3t/9=(ce^3t/9)(3t-1).
J=∫(2t^2e^3tdt): let u=2t^2, du=4tdt. We already have v=e^3t/3 and dv=e^3tdt.
So J=(2/3)(t^2e^3t)-∫(4te^3tdt/3)=(2/3)(t^2e^3t)-(4/3)e^3t(3t-1)/9.
I-J=(ce^3t/9)(3t-1)-(2/3)t^2e^3t+(4/3)e^3t(3t-1)/9=(c-2t)y.
y(c-2t)=e^3t((4/3)(3t-1)/9+c(3t-1)/9-(2/3)t^2).
Apply initial condition y(0)=0: 0=-4/27-c/9, 0=4+3c, c=-4/3, so -2y(2+3t)/3=e^3t((4/3)(3t-1)/9-(4/27)(3t-1)-(2/3)t^2)=-(2/3)t^2e^3t, y(2+3t)=t^2e^3t, y=t^2e^3t/(2+3t).
So y(1)=e^3/5=4.0171 approx.
So we'll come back to this after applying Modified Euler's Method.
EULER
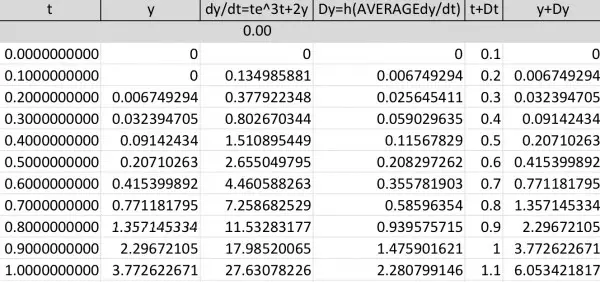
The method seems to give us the answer 3.77 compared with 4.02 from the computed equation, an accuracy of about 93.8%.