The graph of x=y2-6y+8 is a parabola. x=(y-4)(y-2) is another way of writing this, and when x=0 (the y-axis) we have two y intercepts: 2 and 4. x=(y-3)2-1 is another way of writing the equation and it tells us where the vertex is: (-1,3). So the tip of the parabola is intersected by the y-axis, and it's this enclosed tip which is to be rotated. The axis of rotation can be either the x-axis (to create a torus-like solid) or the y-axis (to create a type of football-shaped solid). These are the solids referred to in the question.
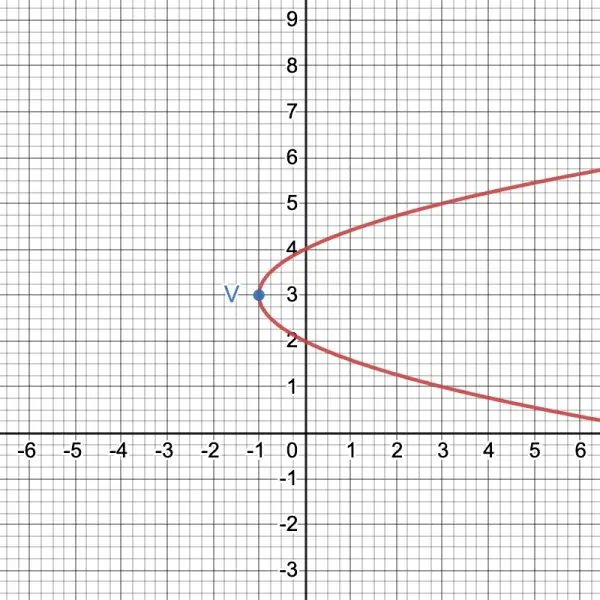
In the picture, V is the vertex (-1,3) and the tip of the parabola lies between x=-1 and the y-axis (x=0).
ROTATION ABOUT THE Y-AXIS
To use the Shell Method, we take a vertical segment through two points P and Q on the parabola. P and Q will have the same x coordinate but will have different y coordinates except at V. For example, when x=0, we have y=2 and y=4. Let P be at (x,y1) and Q be at (x,y2). The length PQ=y1-y2. This will form the wall of a cylinder with thickness dx. The volume of a cylinder is 2πrht where r is the radius, h the height and t the thickness of the wall. So h=y1-y2 and t=dx (infinitesimally thin). We need to find r, which is the distance between the wall and the y-axis, which we can see is the x coordinate, or, rather, -x, because the tip of the parabola is on the negative side of the y-axis. So we have the volume -2πx(y1-y2)dx.
But the y coordinates are the roots of the quadratic y2-6y+8-x=0. We know that (y-3)2=x+1 is another way of writing the equation of the quadratic, so y-3=±√(x+1), y1=3+√(x+1) at P and y2=3-√(x+1) at Q, so PQ=2√(x+1), and the volume of the shell is (-4πx√(x+1))dx. The sum of the volumes of all cylindrical shells is the integral -4π∫x√(x+1)dx and the interval for integration is [-1,0].
To calculate this integral let u2=x+1, then dx=2udu and x=u2-1. When x=-1, u=0 and when x=0, u=1, so the integral becomes -4π∫[0,1]2u2(u2-1)du=-8π∫[0,1](u4-u2)du=-8π[u5/5-u3/3]01=-8π(⅕-⅓)=16π/15.
ROTATION ABOUT THE X-AXIS
This time the solid will be a torus with a limb cross-section formed by the tip of the parabola (resembling a lifebelt as it would appear above the water line). The walls of the cylindrical shells will be horizontal. Their height will be -x and the radius of cylinder will be y. The radius will go from a maximum of 4 to a minimum of 2, and the thickness of the wall will be dy. The volume of a cylinder will be -2πyxdy=-2πy(y2-6y+8)dy.
Volume=-2π∫[2,4](y3-6y2+8y)dy=-2π[y4/4-2y3+4y2]24=-2π(64-128+64-(4-16+16))=8π.