Question

minimize z=4x1+x2

subject to

3x1+x2=3

4x1+3x2≥6

x1+2x2≤4

x1,x2≥0

Answer 1

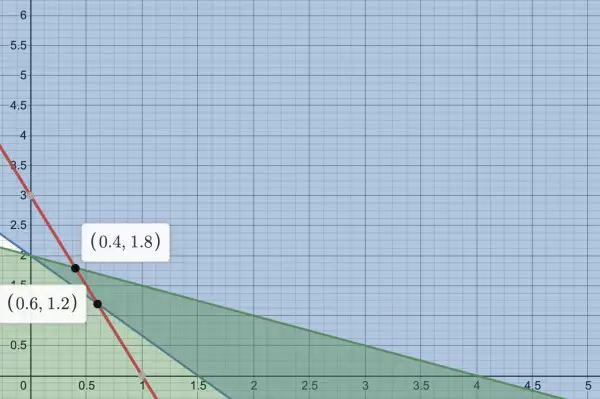
Constraints:

(C1) 3x1+x2=3 (this constraint fixes x2 in relation to x1－see red line on graph)
(C2) 4x1+3x2≥6
(C3) x1+2x2≤4
(C4) x1,x2≥0

C2 and C3 define regions.

From C1, x2=3-3x1, so we can rewrite C2 and C3:

(C2) 4x1+9-9x1≥6, 3≥5x1, x1≤0.6;

(C3) x1+6-6x1≤4, 2≤5x1, x1≥0.4.

Therefore 0.4≤x1≤0.6.

z=4x1+x2 is now applied, that is, z=4x1+3-3x1=x1+3. z is minimum (3.4) when x1=0.4, so x2=3-3x1=3-1.2=1.8.

The graph shows that the possible values of x1 on the horizontal axis must lie on the red line (C1). The minimum value of z occurs at the point (0.4,1.8). The darker shading shows where C2 and C3 are satisfied.