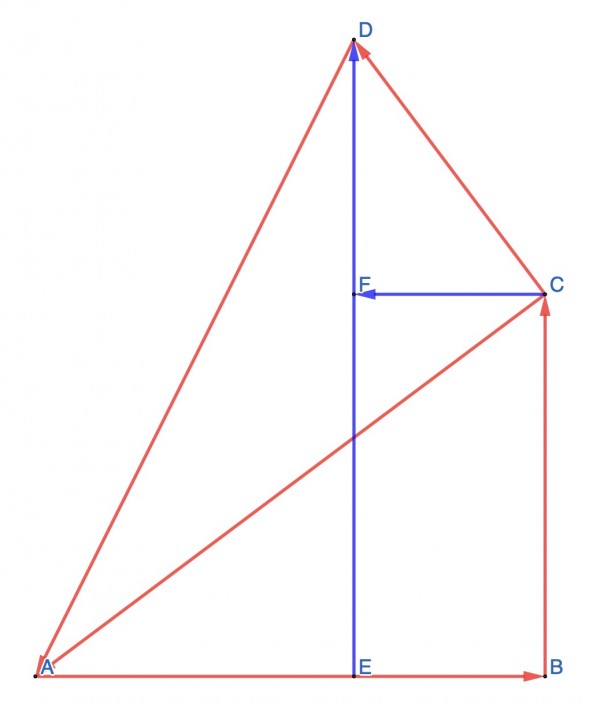
The figure shows two right triangles (red) ACD and ABC. Two construction lines (blue) have been added. DE is perpendicular to AB. CF is perpendicular to DE, forming the rectangle BCFE. The following angles are congruent: CAB, ACF, CDF.
cosDAE=AE/AD=(AB-BE)/AD=(AB-CF)/AD=AB/AD-CF/AD, because BE and CF are opposite sides of the rectangle BCFE. AB/AD can be written (AB/AC)(AC/AD)=cosCABcosDAC; CF/AD=(CF/CD)(CD/AD)=sinCDFsinDAC.
AB/AD=cosDAE=cosCABcosDAC-sinCDFsinDAC. Since CAB and CDF are congruent angles, this can be written:
cosDAE=cosCABcosDAC-sinCABsinDAC and DÂE=DÂC+CÂB;
therefore cos(CAB+DAC)=cosCABcosDAC-sinCABsinDAC.
So for general angles x and y, cos(x+y)=cos(x)cos(y)-sin(x)sin(y).
When x=y: cos(2x)=cos2(x)-sin2(x)=cos2(x)-(1-cos2(x))=2cos2(x)-1.
Therefore 1+cos(2x)=2cos2(x). If x=A/2, then 1+cos(A)=2cos2(A/2) QED