2sin x(x/2) x cos (x/2)=sin x

Question

please show the solution.a

Answer 1

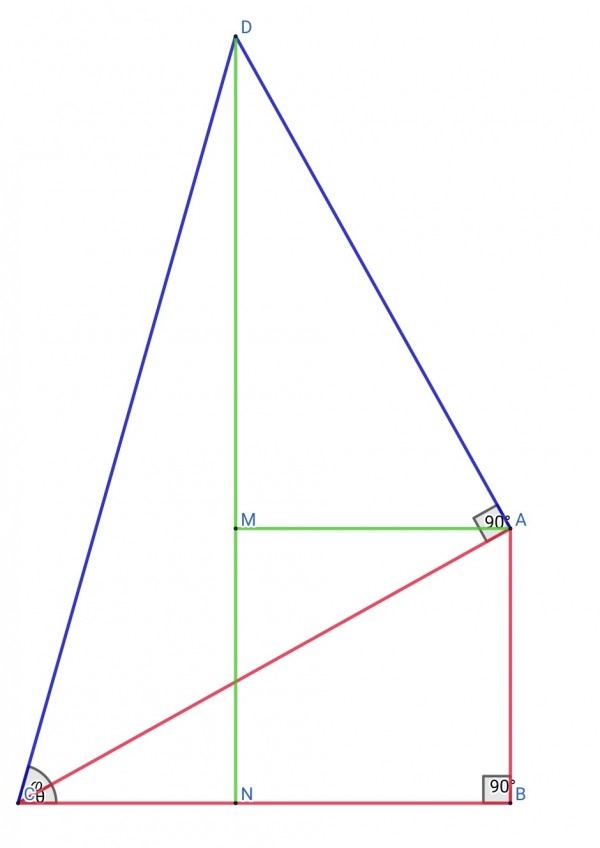
sin(x)=2sin(x/2)cos(x/2) is an identity. We can prove this, but first let's derive another identity. There are two main right triangles in the figure: ABC (red) and DAC (blue with a red base). Let angle ACB=θ and DCA=φ. Using green construction lines I've created more right triangles. Note that angle MAN=MDA=NDA=θ, and we can also see that angle DCB=θ+φ. MABN is a rectangle and DMA and DNC are right triangles.

AC=DCcosφ, MN=AB=ACsinθ=DCcosφsinθ, AD=DCsinφ, DM=ADcosθ=DCsinφcosθ. DN=DM+MN=DCsinφcosθ+DCcosφsinθ.

DN/DC=sinDCB=sin(θ+φ),

so sin(θ+φ)=(DCsinφcosθ+DCcosφsinθ)/DC=sinφcosθ+cosφsinθ.

This is the trig identity for the sine of the sum of two angles. When φ=θ=x/2, sin(θ+φ)=sin(x)=sin(x/2)cos(x/2)+cos(x/2)sin(x/2)=2sin(x/2)cos(x/2). This proves the given identity.