I assume that (1y0,-3) is meant to read (10y,-3). For (5,y) to be equidistant from the two points (5,y) must be the vertex of an isosceles triangle. The midpoint of the other two points is ((10y+1)/2, (4-3)/2), that is, (5y+½,½). (5,y) lies on the perpendicular bisector of the line joining the other two points. The slope of this line is (10y-1)/(-3-4)=(10y-1)/(-7), so the slope of the perpendicular is 7/(10y-1). The perpendicular has to pass through (5,y) and (5y+½,½). The slope of the latter points is (5y+½-5)/(½-y)=(10y-9)/(1-2y).
(10y-9)/(1-2y)=7/(10y-1), (10y-9)(10y-1)=7(1-2y),
100y2-100y+9=7-14y, 100y2-86y+2=0, 50y2-43y+1=0, y=(43±√(1849-200))/100=0.8361 or 0.0239.
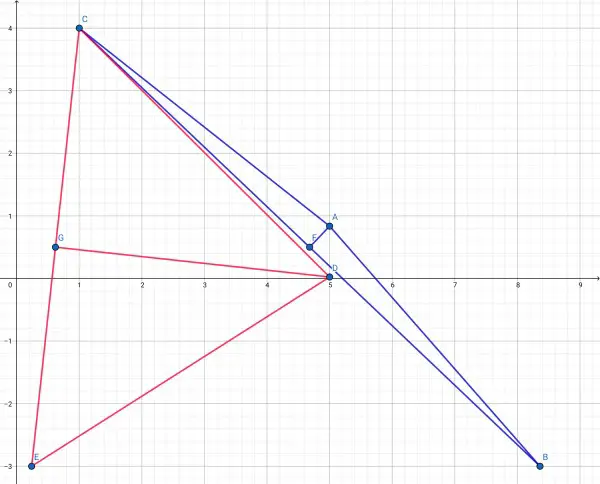
The three points become (5,0.8361), (8.361,-3), (1,4) or (5, 0.0239), (0.2392,-3), (1,4). In the picture below the two isosceles triangles are shown with their perpendicular bisectors (DG and AF) in red and blue. A is equidistant from B and C, and D is equidistant from C and E. A and D represent (5,y) while B and E represent (10y,-3), and C is (1,4).