The picture below shows an aerial view of the conicoid as seen looking down the y axis at the x-z plane. The outer ellipse is the way the conicoid appears at a distance of 3sqrt(5) from the origin, while the inner one is distance 3sqrt(2) from the origin. The origin itself is the point (0,3,0) as seen from above. The straight line is the line z=x, which is the edge view of the plane z=x.
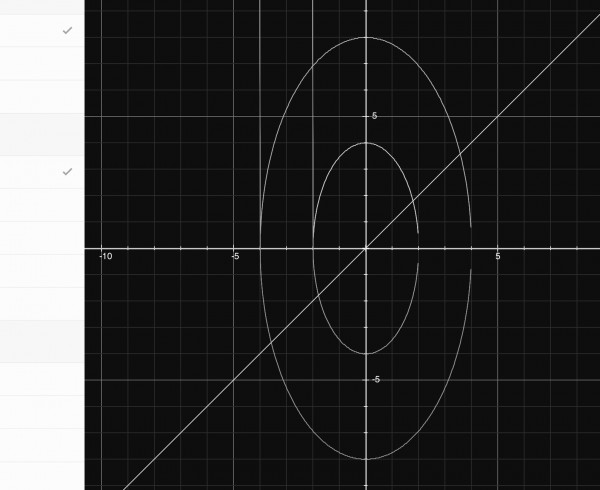
The origin is where the vertex of the conicoid is. The two vertical lines on the left are just markers showing the extent of the ellipse's radius in the x direction. The ellipse's radius in the z direction is 8 for the outer ellipse and 4 for the inner. The picture clearly shows that the plane z=x intersects the conicoid.
This view is also the view looking towards the origin from the negative side of y, because the conicoid is in fact two shapes which are reflections of each other. The origin is the point (0,-3,0).
Now we adjust our viewpoint and look along the other axes to get an idea of other aspects of the conicoid.
Start with the x-y plane, viewed along the z axis. If we treat z in the equation as a constant we can see what the curve looks like for x and y. Initially put z=0: -x^2/4+y^2/9=1 is the equation of a hyperbola, with asymptotes given by x^2/4=y^2/9 or y=±3x/2. These are represented by two lines y=3x/2 and -3x/2, which lie on intersecting planes. When z^2/16+1=4, -x^2/4+y^2/9=4 and the asymptotes are x^2/16=y^2/36, y=3x/2 and -3x/2 as before, and z=4sqrt(3). No matter where we are along the z axis the asymptotes are the same, so the conicoid is contained within these planes. The picture below shows the view along the z axis.
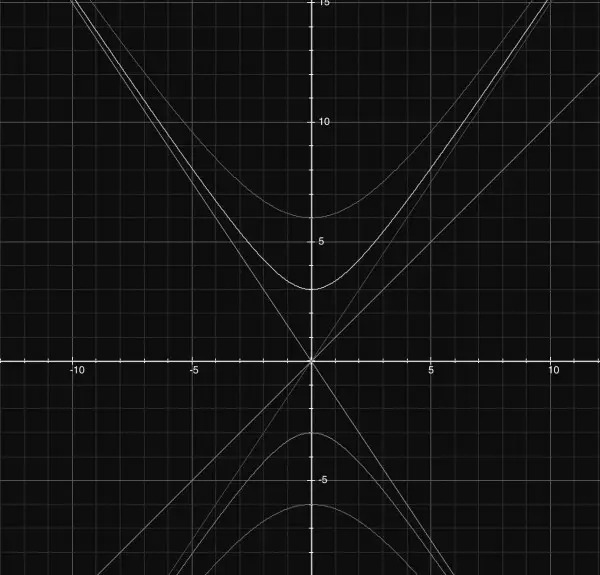
In this picture the line y=x (edge-on view of the plane) misses the conicoid completely, because it lies outside the asymptotes. You can also see the hyperbolas for increasing values of z. The inner hyperbolas are when z=0 and the outer ones are when z=4sqrt(3). By joining one side of each hyperbola to the other with a horizontal line you can visualise the edge-on appearance of the ellipses. These are x-diameters of each ellipse.
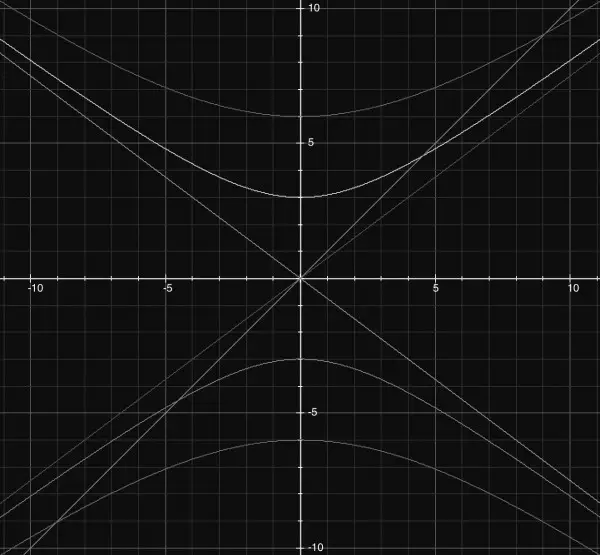
Finally, the view from the x axis. Here the line y=z lies inside the asymptotes so the plane intersects the conicoid.