When z=1, x^2+y^2=4, which is a circle, centre at the origin and radius 2. x-2y=1 is a plane intercepting the x-y plane with y intercept=-1/2 and x intercept=1. The equation x^2+y^2+(z-1)^2=4 is a sphere, centre (0,0,1) and radius 2. The plane cuts through the sphere when (1+2y)^2+y^2=4; 1+4y+4y^2+y^2=4; 5y^2+4y-3=0, y=(-4±sqrt(16+60)/10=0.47178 ((-2+sqrt(19))/5) and -1.27178 ((-2-sqrt(19))/5). These values give x=1.94356 ((1+2sqrt(19))/5) and -1.54356 ((1-2sqrt(19))/5 respectively, by using the equation x=1+2y. So the points of intersection are (1.94356,0.47178) and (-1.54356,-1.27178). From these we can find the diameter of the cylinder: sqrt(76/25+304/25)=sqrt(380)/5=2sqrt(95)/5=3.9 approx. The radius is sqrt(95)/5. The sides of the cylinder are perpendicular to the diameter.
The slope of the diameter is the same as the slope of the plane x-2y=1, which is 1/2, so the slope of the perpendicular is -2. The equations of the sides of the cylinder where z=1 in the x-y plane are y=-2x+c where c is found by plugging in the intersection points: (-2+sqrt(19))/5=-2(1+2sqrt(19))/5+c; -2+sqrt(19)=-2-4sqrt(19)+5c. So c=sqrt(19) and y=sqrt(19)-2x as one side. Similarly, -2-sqrt(19)=-2+4sqrt(19)+5c, c=-sqrt(19) and y=-(sqrt(19)+2x) for the other side.
Consider the view looking along the z axis. The circular cross-section of the cylinder will appear edge on, while the sides will have the slope -2 and will be spaced apart according to the value of z. When z=1±radius of cylinder=1±sqrt(95), the sides will appear to be as one line passing through the x-y plane's origin, the equation of the line being y=-2x when z=1±sqrt(95).
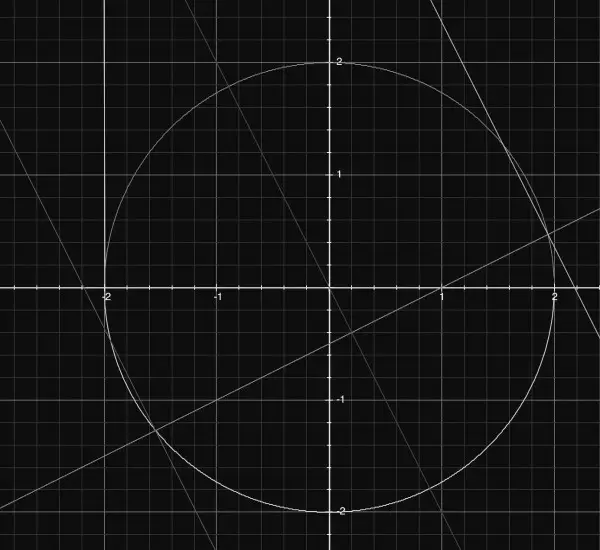
The picture shows the view from z=1 looking at the x-y plane. The circle is the cross-section of the sphere and the line passing through (1,0) and (0,-1/2) is the edge of the plane x-2y=1. The diameter of the cylinder is constant and is shown by the two lines perpendicular to each end of the chord where the plane cuts the sphere. These lines represent the sides of the cylinder as they would appear at z=1. Parallel to them and passing through (0,0) is the single line that appears when z is at the extreme limits of the diameter of the cylinder. This line is also the central axis of the cylinder. (The vertical line at y=-2 is just a marker to show the the leftmost limit of the diameter of the sphere.)
The general equation of a cylinder is the same as the 2-dimensional equation of a circle: x^2+y^2=a^2. This cylinder, radius a, has the z axis its central axis. x^2+z^2=a^2 is a cylinder with the y axis as its central axis. a=sqrt(95)/5 so a^2=95/25=19/5, making the equation of the cylinder 5x^2+5z^2=19. This is the same size as the cylinder in the problem, but with its central axis as the y axis. 5x^2+5(z-1)^2=19 is the equation of the cylinder with central axis passing through the centre of the sphere. If the cylinder is tilted so that its base coincides with the circle produced by the plane cutting through the original sphere, more calculations need to be made to transform the coordinates.
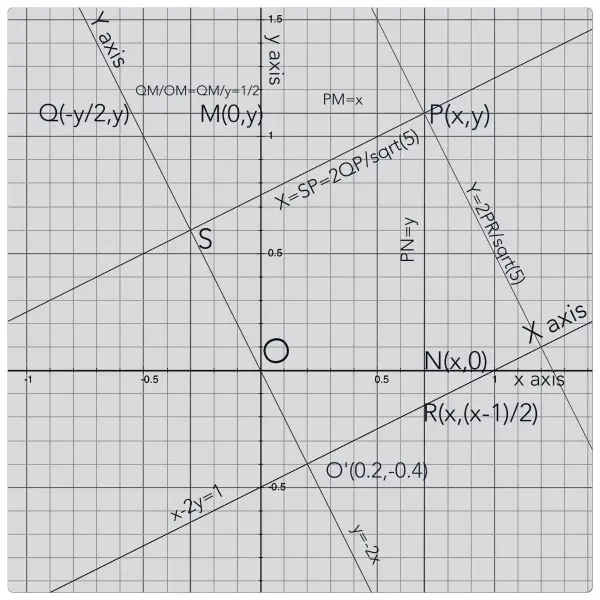
The picture shows the axial tilt of the cylinder. The central axis of the cylinder, y=-2x, bisects the chord on the line x-2y=1 when x-2(-2x)=1; 5x=1, x=1/5. So y=(x-1)/2=-2/5. If x-2y=1 represents the horizontal axis (we'll call X) and y=-2x represents the vertical axis (Y) we can see that, relative to these X-Y coordinates, the cylinder is upright. The z value is unaffected by rotation.
Take a point P(x,y) in the x-y plane. What are its coordinates in the X-Y plane? To find out we use geometry and trigonometry. The axial tilt of the X-Y axes is angle ø where tanø=1/2, so sinø=1/sqrt(5) and cosø=2/sqrt(5).
X=SP=QPcosø=2(x+y/2)/sqrt(5),
Y=PRcosø=2(y-(x-1)/2)/sqrt(5).
Z=z
In the X-Z plane, 5X^2+5Z^2=19.
This transforms to 4(x+y/2)^2+5z^2=19=(2x+y)^2+5z^2.
In the X-Y plane the sides of the cylinder are the lines X=-a and X=a, where a^2=19/5. So X^2=19/5, which transforms to 4(x+y/2)^2 or (2x+y)^2=19/5; 2x+y=±sqrt(3.8), corresponding to the equation of two parallel, sloping line forming the sides of the cylinder.