Let H=number of history students, G=number of geography students, P=number of students who passed. Draw 3 interlocking circles for H, G and P, to make 7 regions in a Venn diagram. Enclose the interlocking circles in a big circle indicating all students (not shown). Two regions are empty: there are no students passing in any other subject and all students are included in the interlocking circles, there are no students outside these. Later, I assume and identify some other empty regions (sets).
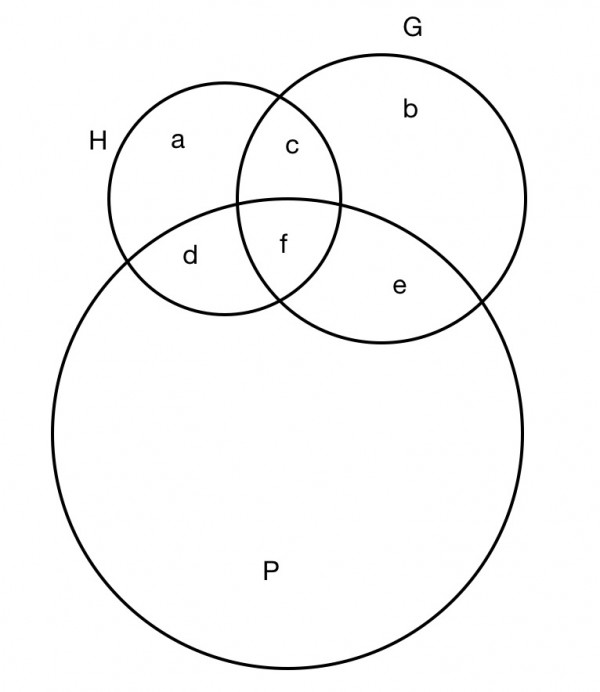
(Relevant sets shown above.)
Define 7 regions (sets) a-g:
a History only taken but not passed (see later)
b Geography only taken but not passed (see later)
c History and geography taken but not passed (see later)
d History passes
e Geography passes (d+9)
f History and geography passes (75)
g All students (158)
g=a+b+c+d+e+f=158=a+b+c+2d+9+75
Assume a=b=c=0, because all students passed in one or other subjects, or both, then 2d=74 and d=37, so e=46.
So 37 students took and passed history, and 46 took and passed geography, but not both subjects.
We can calculate H=a+c+d+f=37+75=112 (all history students); G=b+c+e+f=46+75=121 (all geography students). P=158 (all students passed).