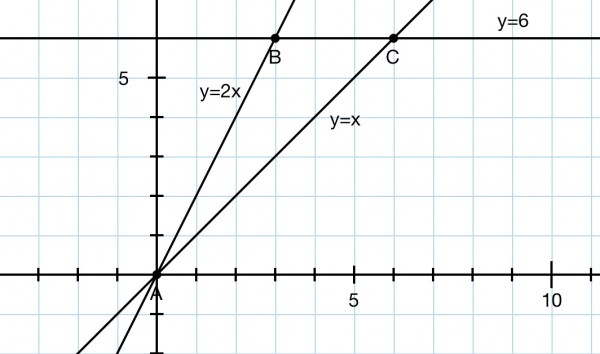
The enclosed area is the triangle ABC.
To find the volume of ABC rotated about the y axis, consider a "washer" with inner radius x where x=y/2 and outer radius x where x=y. The area of the washer is π(y^2-y^2/4)=3πy^2/4 and volume 3πy^2dy/4, where dy is the infinitesimal thickness.
The volume of ABC rotated is (3π/4) ∫(y^2dy) for 0≤y≤6=(3π/4)[y^3/3] for 0≤y≤6=(π/4)*216=54π cu units=169.65 approx.
An alternative approach is to consider the volumes of two cones. The volume of a cone is πr^2h/3 where r is the radius and h the height. So we have for the outer cone: V=π(6^2)6/3=72π and for the inner cone: V=π(3^2)6/3=18π, so the difference is 72π-18π=54π.