Triangle abc has angle b is equal to angle c.prove that the perpendicular from midpoint of bc to ab and ac are equal. The perpendicular from b and c to the opposite side are equal

Question

Ninth icse

Answer 1

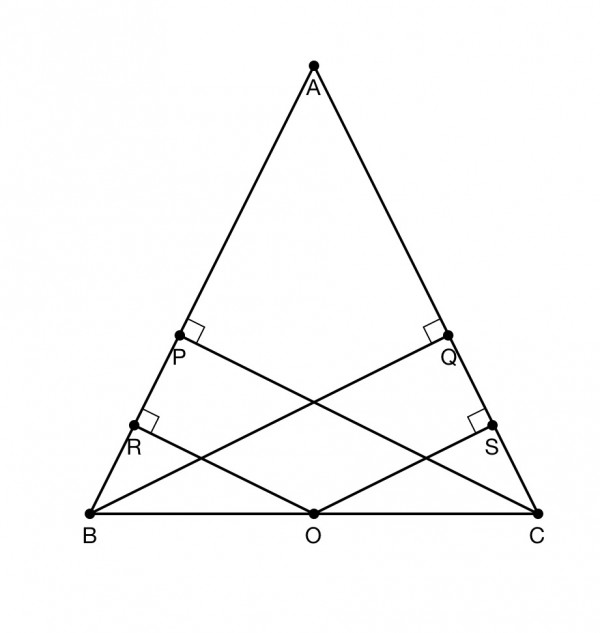
The picture shows an isosceles triangle fitting the description.

BO=OC (because O is the midpoint of BC).

BRO=OSC=90º by definition.

Angle ABC=ACB (given, equal angles of triangle ABC).

Angle ROB=SOC=90-ABC=90-ACB (angles in a right-angled triangle).

Triangles ROB and SOC are congruent because all the angles and the hypotenuses are equal.

Therefore OR=OS and BR=SC.

Angle PCB=90-ABC and angle QBC=90-ACB so PCB=QBC.

BC is common to triangles BPC and BQC. Angle BPC=BQC=90º by definition.

Triangles BPC and BQC are congruent (all angles and hypotenuses are equal).

Therefore PC=BQ.