A(4,7) is the vertex of triangle ABC. BA=(5,3) and AC=(4,-3). (a) find the coordinates of B and C . (b) if M is the midpoint of the line BC, find AM.

Question

Draw your own rough sketch

Answer 1

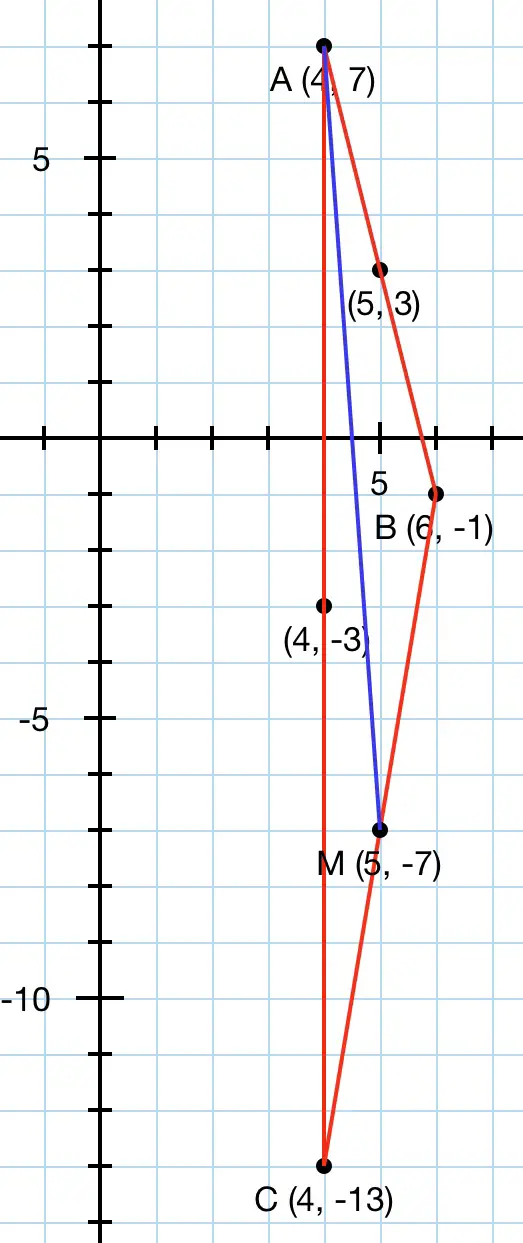
My interpretation of this problem is shown above. I have assumed that the point BA is the midpoint of line BA and the point AC is similarly the midpoint of AC. The vertices B and C are B(6,-1) and C(4,-13) are shown as calculated from the midpoints. M is the point (5,-7). The length of AM is found using Pythagoras’ Theorem: M is 1 unit away from the vertical AC. The perpendicular from M to AC is 14 units from A. Therefore AM²=14²+1²=197 so AM=√197=14.0357 approx.