village A,B,C,D are such that B is 4km due east of A,C is 3km due south of B and D is 4km S50W from C

Question

Calc the distance and bearing of A and D

Answer 1

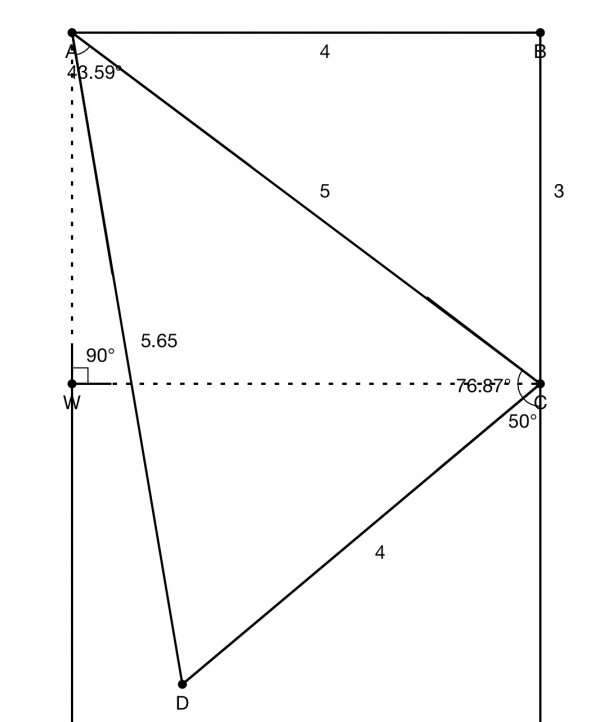
AC=√(AB^2+BC^2)=√(16+9)=√25=5km. Angle ACW=BAC=arctan(3/4)=36.87º approx. and ACD=40+36.87=76.87º.

Cosine rule: AD^2=5^2+4^2-40cos76.87=31.9135 approx, so AD=5.65km approx. 

Sine rule: sinDAC/4=sinACD/AD=0.1724 approx, making sinDAC=0.6896 and DAC=43.59º.

The bearing of D from A is 43.59+36.87=80.46° S of E or N170.46 or 9.54° E of S.