Probability problem

Question

 In John’s cattle pound, there are 5 bulls and 15 cows. In Jane’s cattle pound,
there are 2 bulls and 8 cows. John and Jane agree to exchange one animal
each. After John randomly selects one animal and sends it to Jane, Jane
randomly selects one animal and sends it to John.

(i) Draw the relevant sample space in a tree diagram.

(ii) Using it, find the probability of each of the following events.
     (a) There being a reduction in the number of bulls in John’s pound
         because of the exchange
     (b) There being an increase in the number of bulls in John’s pound
         because of the exchange
     (c) There being no difference in the number of bulls and cows in each of the
         two pounds because of the exchange

(iii) Now suppose they exchange animals in a way different to that mentioned
      above. Suppose John and Jane randomly take one animal from each of
      their pounds and go to their friend Adam’s house and exchange the cattle
      there and bring the exchanged cattle back to the pound. Find the probabilities
      of the events given in (ii) above for this random experiment. 

Answer 1

Tree diagrams added. I hope my revised calculations are correct.

PART A and PART B correspond to (iii) in the question; PART A involves John and Jane only and PART B involves John, Jane and Adam. 

PART A

John's probability of picking a bull from his cattle is 5/20=1/4 and 3/4 for a cow. After receiving one animal from John, Jane now has 11 animals in two scenarios (B=bull, C=cow):

Jane receives a bull: 3B+8C: Jane's probability of picking a bull from her cattle is 3/11 and 8/11 for a cow.

Jane receives a cow: 2B+9C: Jane's probability of picking a bull from her cattle is 2/11 and 9/11 for a cow.

(i) Loss and gain from John's point of view:

1. -B+B=0→(5B+15C,2B+8C), p=1/4 * 3/11=3/44=0.0682

2. -B+C→(4B+16C,3B+7C), p=1/4 * 8/11=2/11=0.1818

3. -C+B→(6B+14C,B+9C), p=3/4 * 2/11=3/22=0.1364

4. -C+C=0→(5B+15C,2B+8C), p=3/4 * 9/11=27/44=0.6136

Note that 3/44+2/11+3/22+27/44=1.

These are the 4 leaves of the tree of probabilities. There are 4 possible outcomes.

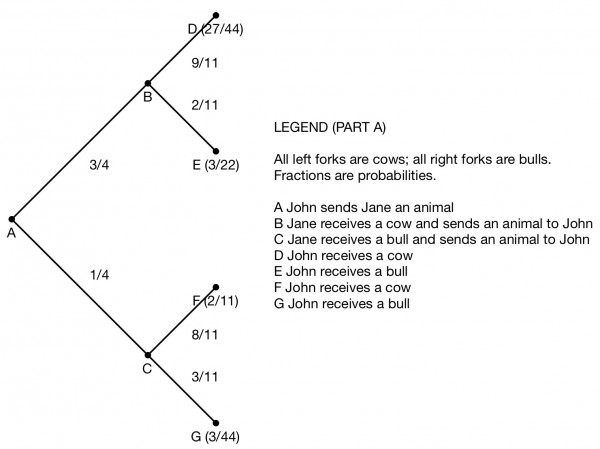
On the tree diagram multiply the probability fractions encountered on the path to a particular leaf. This product is shown on the leaves at D, E, F and G. For example, if we take the path ACF, we are saying that John sends Jane a bull and Jane sends John a cow, probability p=1/4*8/11=2/11, leaf2 (point F in the diagram) in the sample space.

Sample space of animal configurations with ordered pairs (John's cattle,Jane's cattle):

{ (5B+15C,2B+8C) (4B+16C,3B+7C) (6B+14C,B+9C) (5B+15C,2B+8C) }

Corresponding sample space of probabilities:

{ 3/44 2/11 3/22 27/44 } 

(ii)

 (a) leaf2=2/11

 (b) leaf3=3/22

 (c) leaf1+leaf4=3/44+27/44=15/22

PART B

John's probability of picking a bull from his cattle is 5/20=1/4 and 3/4 for a cow as in PART A.

Jane's probability of picking a bull from her cattle is 2/10=1/5 and 4/5 for a cow. This differs from PART A.

(i) Loss and gain from John's point of view:

1. -B+B=0→(5B+15C,2B+8C), p=1/4 * 1/5=1/20=0.05

2. -B+C→(4B+16C,3B+7C), p=1/4 * 4/5=1/5=0.2

3. -C+B→(6B+14C,B+9C), p=3/4 * 1/5=3/20=0.15

4. -C+C=0→(5B+15C,2B+8C), p=3/4 * 4/5=3/5=0.6

Note that 1/20+1/5+3/20+3/5=1.

These are the 4 leaves of the tree of probabilities. There are 4 possible outcomes.

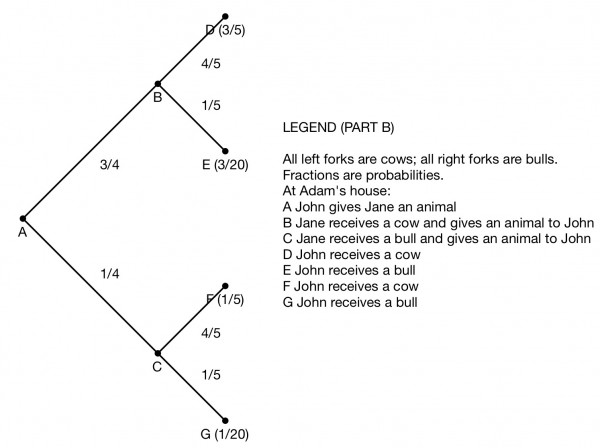
Sample space of cattle with ordered pairs as before:

{ (5B+15C,2B+8C) (4B+16C,3B+7C) (6B+14C,B+9C) (5B+15C,2B+8C) }

Corresponding sample space of probabilities:

{ 0.05 0.2 0.15 0.6 }

(ii)

 (a) leaf2=1/5=0.2

 (b) leaf3=3/20=0.15

 (c) leaf1+leaf4=1/20+3/5=13/20=0.65

Comments

Thank you so much Rod. Please can you say how to draw tree diagram for this.

---

Give me some time and I'll work one out. Probably some time tomorrow.

---

Great. Thank you