Show that ABCD is a parallelogram

Question

In quadrilateral ABCD, diagonals AC and BD intersect at E such that

         AE:EC=BE:ED

Show that ABCD is a parallelogram.

Answer 1

 

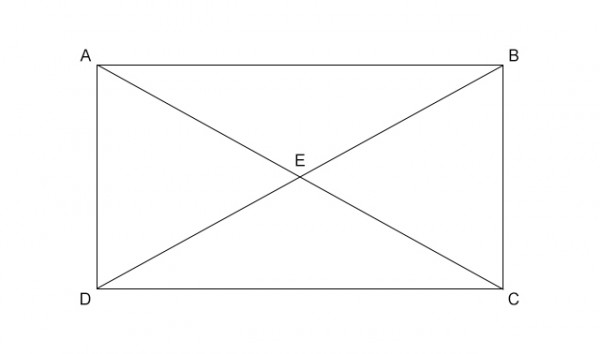
In  triangles ABE and CDE,

AE/EC = BE/ED (Because AE:EC=BE:ED)                                                                                                        So triangles ABC and APQ are equiangular.

Then angles BAE = DCE, So AB//DC (Becasue angles BAE = DCE are alternate angles and they are equal)

 

Also in  triangles ADE and BCE,

AE/EC = BE/ED (Because AE:EC=BE:ED)                                                                                                        So triangles ADE and BCE are equiangular.

Then angles CBE = ADE, So AD//BC (Becasue angles CBE = ADE are alternate angles and they are equal)

So ABCD is a parallelogram (since pairs of opposite sides are parallel)