Please note that the title to this question has y=f(x)=x^3-3x+2 but the text of the question has y=f(x)=3x^3-3x+2, which is the equation I have used in my answer.
(a)
1. f'(x)=dy/dx=9x^2-3 using the rules of differentiation
2. f"(x)=18x (gives the nature of any turning point)
3 and 4: f'=0 at a turning point, so 9x^2=3 and x^2=1/3 so x=±1/√3 or ±√3/3 in rational form. When x>0 f">0 and when x<0 f"<0. This means that x=√3/3 is a minimum and x=-√/3 is a maximum.
5. There is no point of inflexion.
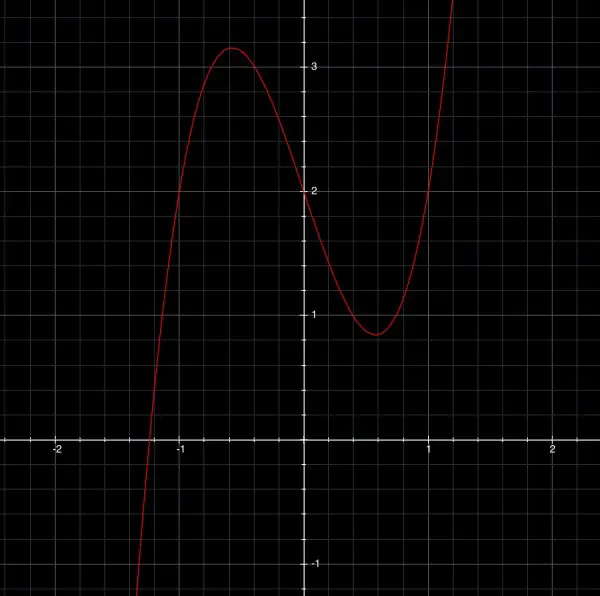
6. The graph is shown below. The intercepts are y=2 and the root(s) of 3x^3-3x+2=0. They only point where the curve intercepts the x axis is about x=-1.24.
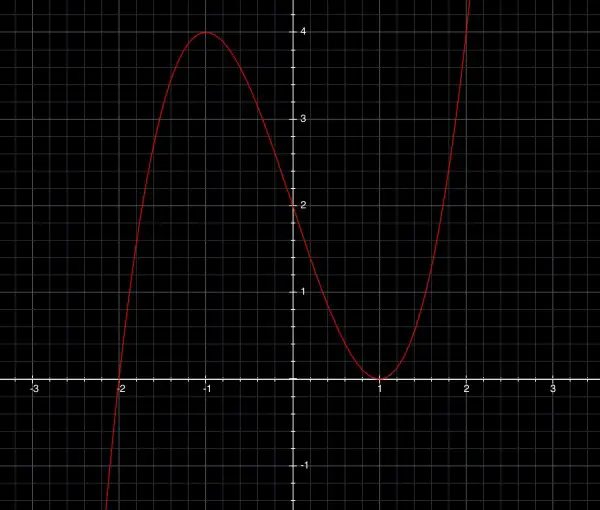
If f(x)=x^3-3x+2 was the intended equation, the graph will look similar (not the same) but all the answers will not fit. Nevertheless I think you can work out the answers for yourself given the general idea of how to do so in this solution. The major difference is that x^3-3x+2 factorises: (x+2)(x-1)^2 with roots x=-2 and x=1 (x intercepts, so the curve cuts or touches the x axis twice). Also the max and min are at x=±1 (max at x=-1 and min at x=1). The graph below of x^3-3x+2 clearly shows the intercepts with the curve just touching (not intercepting) the x axis at x=1, while x=-1 is a clear intercept. The turning points are (-1,4) (max) and (1,0) (min).
If you would like a full solution to this, add a comment to this answer and I will answer using a comment reply.