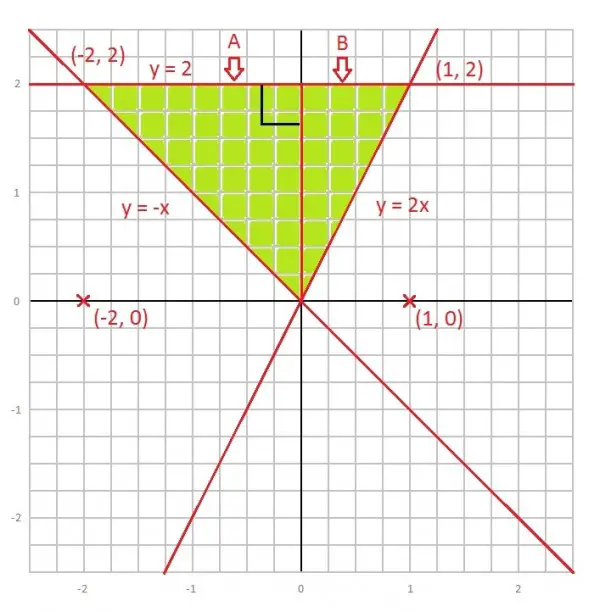
Problem: what is the area and perimeter of a triangle with the lines y=-x, y=2x, y=2
it is a algebraic question
As you can see in the image, there are two right-triangles. We can calculate
the length of each hypotenuse with the Pythagorean Theorem.
For triangle A:
c^2 = a^2 + b^2
c^2 = 2^2 + 2^2
c^2 = 4 + 4
c^2 = 8
c = sqrt(8)
c = 2.828
For triangle B:
c^2 = a^2 + b^2
c^2 = 1^2 + 2^2
c^2 = 1 + 4
c^2 = 5
c = sqrt(5)
c = 2.236
The length of third side of this larger triangle is 3. We add
the three lengths to get the perimeter:
3 + 2.828 + 2.236 = 7.064
We also use the two right-triangles to calculate the area of the
larger triangle.
For triangle A:
a = 1/2 * b * h
a = 1/2 * 2 * 2
a = 2
For triangle B:
a = 1/2 * b * h
a = 1/2 * 1 * 2
a = 1
Adding these we get the area of the larger triangle:
a = 1 + 2
a = 3
Answer: area = 3 square units, perimeter = 7.064 units
I say units because we don't know whether these are inches,
centimeters, yards, etc.