A rectangle has maximum area when length=width, that is, the rectangle is a square.
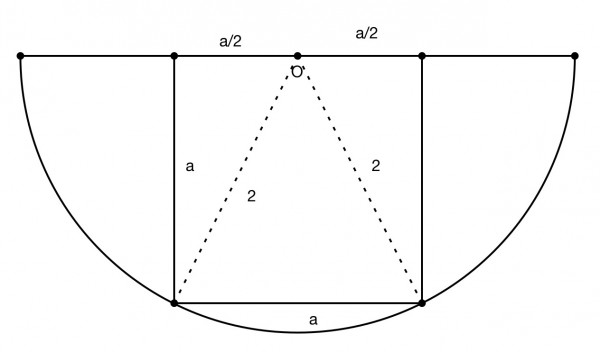
The picture shows the inscribed square. The radii are shown as dotted lines. The centre of the semicircle O is also the midpoint of a side of the square, of side a. Therefore by Pythagoras a^2+(a/2)^2=4.
5a^2/4=4 so area=a^2=16/5=3.2 and a=4/√5 or, rationally, 4√5/5=1.789.
Proof that a square is the shape a rectangle must be to have maximum area is as follows.
Let the length of the rectangle be a+x and the width be a-x (a is simply the average of length and width).
Area = (a+x)(a-x)=a^2-x^2. This expression is maximum when x=0, so length=width=a. This makes the rectangle a square.