prove that C,D,H,E are concyclic

Question

Two circles intersect at points A and B. From a point p on the common chord BA produced, secats PEH and PCD are drawn to each circle . Prove that C,D,HE are concyclic.

Answer 1

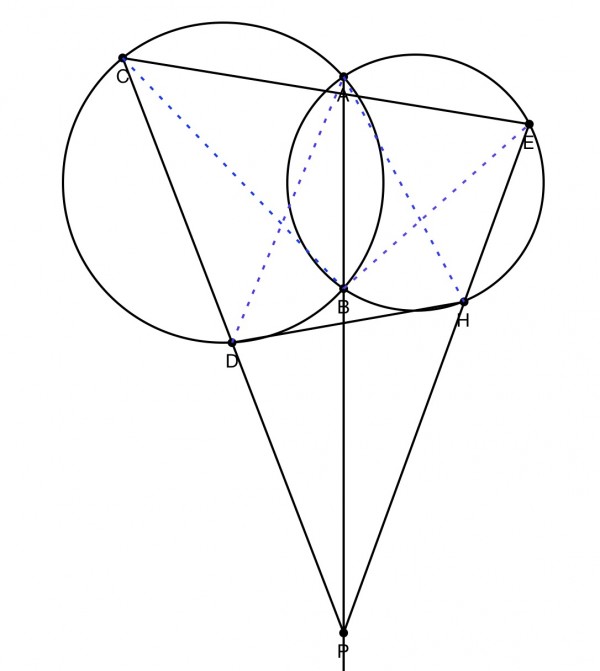
The picture shows the secants from point P.

The quadrilateral CDHE is required to be proved to be a cyclic quadrilateral. That means that CDH+CEH=180=DCE+EHD.

Join CB and AD, and join AH and BE. From this construction we get two pairs of similar triangles: APD and BPC, and APH and BPE, because of the common angle at P, and equal angles PCB=DAP, PAH=BEP (angles in the same segment).

We can therefore write:

PD/PB=PA/PC=DA/BC (triangles PCB and DAP) and PB/PH=PE/PA=BE/HA (triangles PAH and BEP).

From this we get: PB.PA=PC.PD=PE.PH.

So PC.PD=PE.PH and therefore PC/PE=PH/PD. Therefore, triangles PCE and PHD are also similar because P is the included common angle. This means PDH=PEC. But CDH=180-PDH (supplementary angles on a straight line), so CDH=180-PEC (PEC is the same angle as CEH). These are opposite angles of the quadrilateral CDHE, and this is a definitive property of cyclic quadrilaterals, so CDHE is cyclic. The other two angles must also be supplementary because the angles of a quadrilateral add up to 360 degrees.